A
fim de mostrar que as duas retas  são assíntotas à hipérbole, verifiquemos o seguinte:
são assíntotas à hipérbole, verifiquemos o seguinte:
-
para x>0 e muito grande, a distância entre o gráfico de 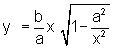 e
de
e
de 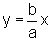 tende a
zero.
tende a
zero.
De fato, para um mesmo valor de abscissa, temos que a diferença das ordenadas é:
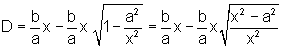
colocando o fator 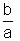 em evidência e usando o fato que
em evidência e usando o fato que  porque x>0,
porque x>0,
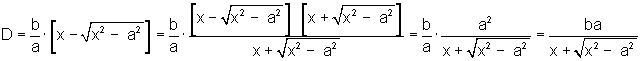
onde multiplicamos o numerador e o denominador por 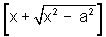 ,
a fim de calcular o limite quando x se torna muito grande, isto é, tende
a infinito, escapando da situação de indeterminação.
,
a fim de calcular o limite quando x se torna muito grande, isto é, tende
a infinito, escapando da situação de indeterminação.
Assim, quando x tende a infinito, temos que D tende a zero, ou, em notação de limite,
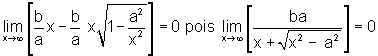
Da
mesma forma, 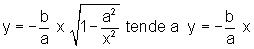 quando
quando
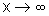 .
.
- Para x<0, x muito
grande em valor absoluto, pode-se mostrar analogamente
que a distância entre  e entre
e entre
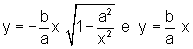 também tende a zero quando
também tende a zero quando 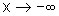 .
.
Dessa maneira, mostramos
que as retas 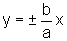 são assíntotas à hipérbole
são assíntotas à hipérbole 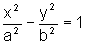 .
.
 |
