A função inverso de um número real não nulo é expressa na forma .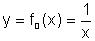
Para cada valor da variável independente x, 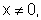temos determinado, em correspondência, o valor de seu inverso. Esta função tem uma característica importante, pois o seu domínio é o conjunto R*, ou seja, os números reais diferentes de zero.

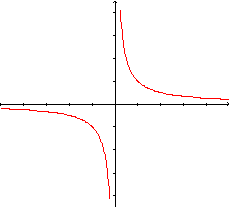
O gráfico dessa função é uma curva denominada hipérbole.

Na busca de funções do mesmo tipo, porém mais gerais, podemos examinar as transformações possíveis em termos de translações - verticais ou horizontais - ou mudanças de inclinação.

Em primeiro lugar, podemos considerar 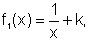definida para 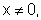com k constante. Seu gráfico comparado ao da função 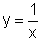levanta uma questão natural: qual a ação da constante k no gráfico da nova função quando comparado ao gráfico da função inicial?


Outra função do mesmo tipo pode ser obtida quando consideramos 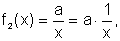com o coeficiente a não nulo, novamente definida para 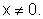Se a=0, a função obtida será a função constante nula, que não interessa nesse momento.

Atribuindo diferentes valores para a, podemos estabelecer uma conclusão a respeito da ação do coeficiente a no gráfi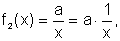co de quando comparado ao gráfico de .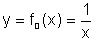

Podemos, em seguida, considerar funções do tipo 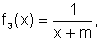onde m é um número real não nulo, definidas para 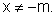Observemos, por exemplo, o gráfico de 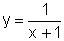em comparação ao gráf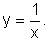ico de

Esboçar o gráfico de .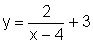

Finalmente, quando a função racional está dada na forma 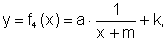as transformações realizadas a partir de 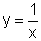são facilmente identificadas e, esboçar o gráfico, não deve causar problema algum.

De fato, consideramos 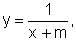em seguida, 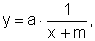e, finalmente, 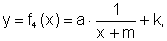. Observe que o coeficiente a não pode ser zero. Por quê ?

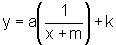
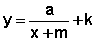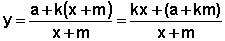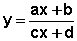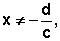Observemos agora que pode ser escrito na forma que nos leva a estabelecer a seguinte conjectura: será que uma função mais geral do tipo , definida para pode ser obtida a partir de 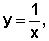realizando transformações como as que acabamos de verificar, ou seja, translações ou mudanças de inclinação?

A resposta é, de fato, afirmativa. Vejamos, inicialmente, um exemplo.

A função 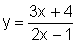definida pa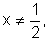ra pode ser escrita da seguinte maneira:

.

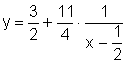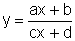De modo geral então, , com 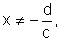pode ser obtida a partir de 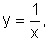uma vez que pode ser escrita na forma

y= .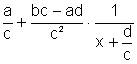


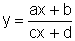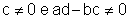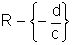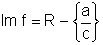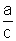Conclusão: A função, , com tem domínio o conjunto , pois o denominador não pode ser nulo. A imagem é o conjunto , pois a variável dependente y não poderá ser igual a , devido à restrição imposta na definição da função.


Observamos que o estudo dos gráficos das funções envolvidas ajuda na resolução de equações ou inequações, pois as operações algébricas a serem realizadas adquirem um significado que é visível nos gráficos das funções esboçados no mesmo referencial cartesiano.