A
curva 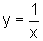 tem
o seguinte aspecto:
tem
o seguinte aspecto:
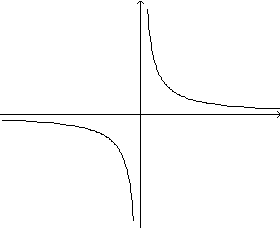
e, portanto, apresenta:
-
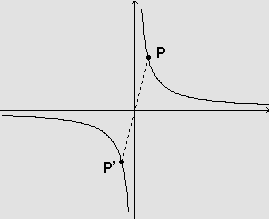
Simetria em relação à origem O=(0,0).
De fato: se o ponto P=(a,b) pertence à curva - isto é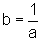 ,
então, o ponto
,
então, o ponto
P'=(-a,-b) também pertence, pois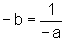 .
É claro que d(P,O)=d(P',O), pois
.
É claro que d(P,O)=d(P',O), pois 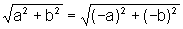 .
.
-
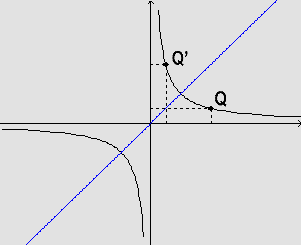
Simetria em relação à reta r: y=x. De fato: se o ponto Q=(c,d) pertence à curva - isto é
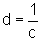 - então o ponto Q'=(d,c) também pertence, pois
- então o ponto Q'=(d,c) também pertence, pois 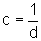 .
Também
d(Q,r)=d(Q',r).
.
Também
d(Q,r)=d(Q',r).
-
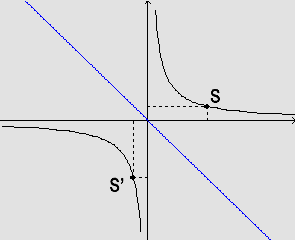
Simetria em relação à reta s: y=-x.
De fato: se o ponto S=(e,f) pertence à curva, isto é,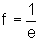 ,
então o ponto
,
então o ponto
S'=(-f,-e) também pertence, pois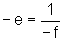 . Também
de modo análogo, é possível mostrar que d(S,s)=d(S',s).
. Também
de modo análogo, é possível mostrar que d(S,s)=d(S',s).