![]()
Consideremos
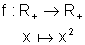
ou seja, a função que a todo número real não negativo associa o seu quadrado. Neste caso, podemos definir
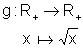
que,
a todo número real não negativo x, associa um outro número, cujo quadrado
é o x dado inicialmente.
Assim, temos:
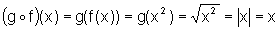 .
.
Basta
observar que, como 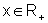 = Domf, x
= Domf, x 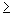 0 e, portanto,
0 e, portanto, 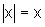 .
.
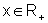 = Domf, x
= Domf, x 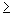 0 e, portanto,
0 e, portanto, 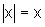 .
.Também temos:
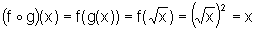
Dessa forma, dada f, encontramos g, tal que,
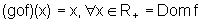
e
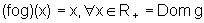 ,
,
ou seja, ambas as composições fornecem a função identidade, Id(x)=x, para
todo 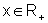 .
Assim g é a inversa de f e f é a inversa de g.
.
Assim g é a inversa de f e f é a inversa de g.
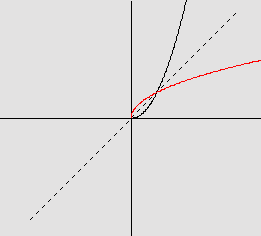
Graficamente, colocando f e g num mesmo par de eixos, temos:
 |
