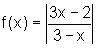
Temos:

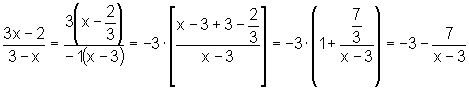
e, portanto,

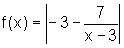
ou seja:

ou ainda

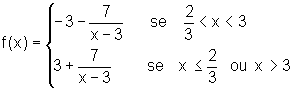
Assim,

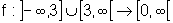
Esboçando o gráfico de f, temos:

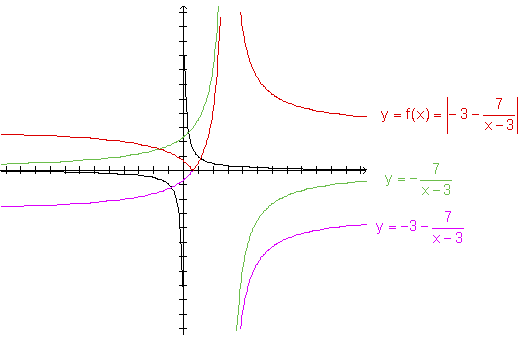
A partir do gráfico, observamos que f não é inversível, pois não é injetora. Vamos considerar as possíveis restrições do domínio a fim de obter duas funções inversíveis:

Observemos que y=0 quando .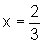

Dom f1=

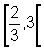e Dom f2=

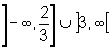Além disso, é conveniente observar que f₂ é a rebatida da função original restrita ao intervalo dado em Dom f₂, enquanto que f₁ é a função original restrita ao intervalo dado em Dom f₁.

Quando x percorre o Dom f₁, temos:

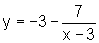
e, portanto,

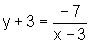
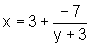
ou seja,

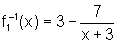, sendo

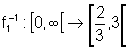
Por outro lado, quando x percorre Dom f₂, temos:

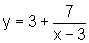
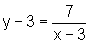
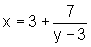
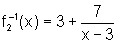, sendo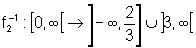

Graficamente, temos:

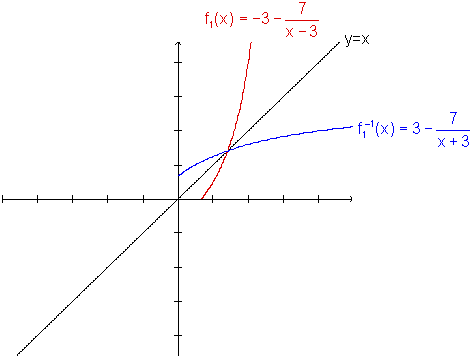
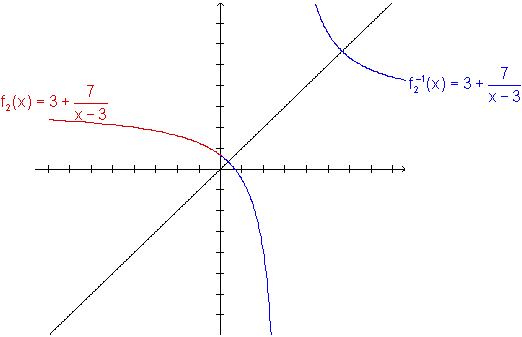
Nesta última figura, é preciso tomar cuidado na análise, uma vez que o gráfico da função f₂ apresenta simetria com relação à bissetriz y=x, e, portanto, houve uma sobreposição parcial dos gráficos de f₂ e de sua inversa.