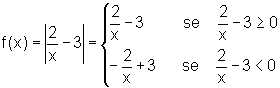
Observe que, quando a função é dada através de um módulo, na verdade, estão sendo dadas duas funções, cada uma delas definida em determinado domínio. Sendo assim, podemos escrever:
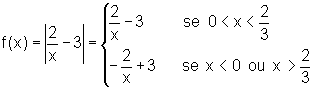
Assim,
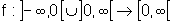
Esboçando o gráfico de f, temos:
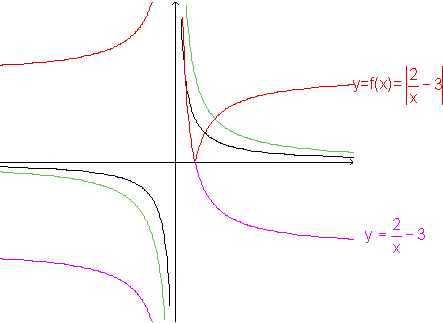
Observação:
Uma dúvida pode surgir a partir do gráfico: será que as curvas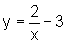 
e 
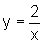se encontram?
,
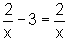teríamos, evidentemente, um absurdo!
Observe
que y = 0 quando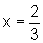 
.
A partir do gráfico, observamos também que f não é inversível, pois não é injetora. Vamos considerar as possíveis restrições do domínio a fim de obter duas funções inversíveis:
Dom
f1 = |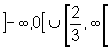
e
Dom f2
= 
|
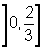
Além disso, é conveniente observar que f1 é a rebatida da função original restrita ao intervalo dado em Dom f1, enquanto que f2 é a função original restrita ao intervalo dado em Dom f2.
Quando x percorre Dom f1, temos:
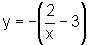
e, portanto,
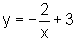
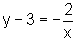
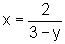
ou seja,
,
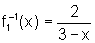sendo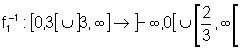 
Por outro lado, quando x percorre Dom f2, temos:
,
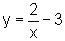
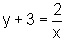
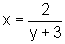
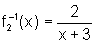sendo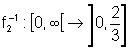 
Graficamente, temos:
 |
 |
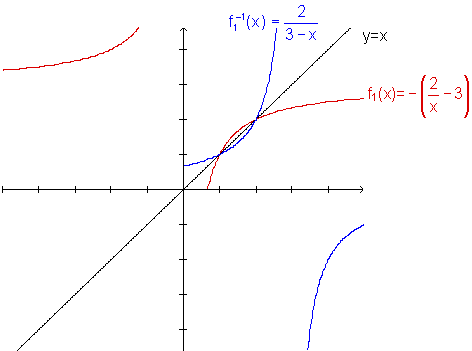
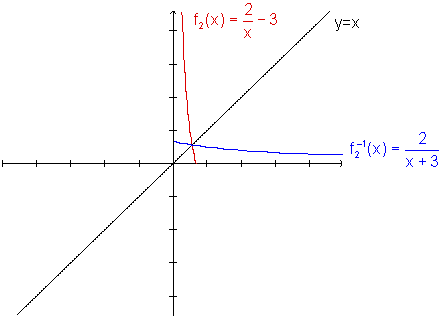