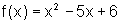
Completando quadrados, temos:
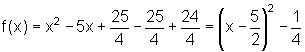
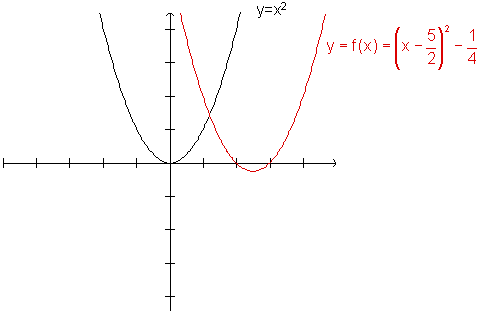
Observe
que desenhamos a curva inicial y=x2 e
aquela obtida após as duas translações, horizontal
de 
e vertical
de 
, 
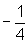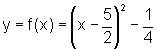, que é o gráfico da função dada.
Temos
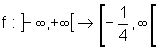, sendo que
a função não é inversível em seu domínio,
pois não é injetora.
Podemos, no caso, considerar duas restrições f1 e f2 de modo que:
Dom
f1 = |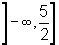
Dom
f2 = |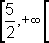
Vamos determinar as respectivas expressões das inversas de f1 e f2.
Temos:
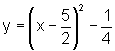
ou seja,
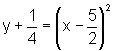
e, extraindo a raiz quadrada de ambos os termos da igualdade, obtemos
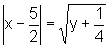
isto é,
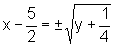
Logo,
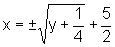
Portanto,
e
Observe
que o domínio das funções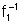 
e 
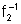é
o mesmo e é justamente a imagem de f.
Graficamente, temos:
 |
 |
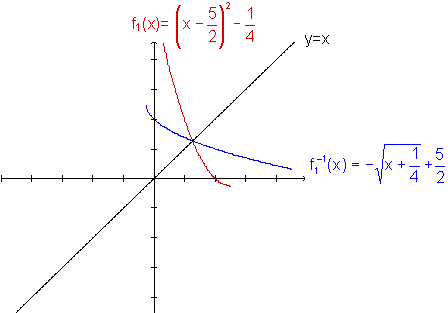
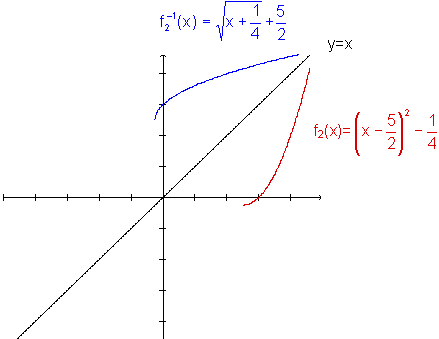