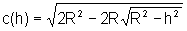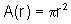
Isolando r, obtemos 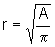, uma vez que r é um número positivo.
Logo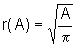

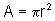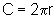Como e , temos:

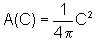
O volume da esfera é dado por 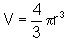e a área da superfície esférica é dada por 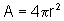. Assim, isolando r na segunda relação e substituindo na primeira, temos

Deixando explícito o fato que V é uma função de A, temos:

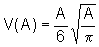
O volume de um cilindro de altura h e raio da base r é dado por .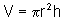
Isolando h e deixando explícito o fato que h é uma função de V, temos:

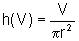
O volume de um cone de altura h e raio da base r é dado por .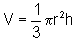

Deixando explícito o fato que V é uma função de r, sendo h dado, temos:

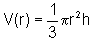
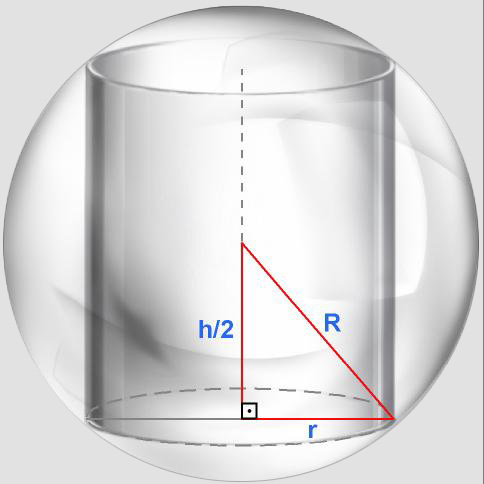FIGURA1

O volume de um cilindro de altura h e raio da base r é dado por 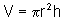. Sendo h dado, e sabendo que o cilindro está inscrito numa esfera de raio R dado, podemos descrever o raio da base do cilindro na dependência de h e R, obtendo:

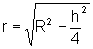
Substituindo r e, explicitando o fato que V é uma função de h, temos:

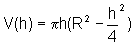
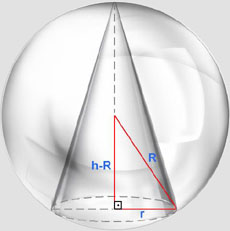FIGURA 2a

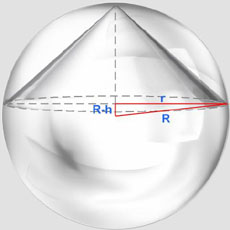FIGURA 2b

O volume de um cone de altura h e raio da base r é dado por 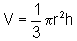. Sendo h dado, e sabendo que o cone está inscrito numa esfera de raio R dado, podemos descrever o raio da base do cone na dependência de h e R, obtendo:

Substituindo r e, explicitando o fato que V é uma função de h, temos:

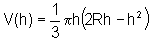
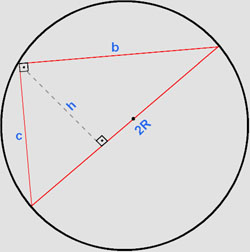FIGURA 3

Como o triângulo é retângulo, sua hipotenusa é um diâmetro da circunferência na qual ele está inscrito.

Por outro lado temos (2R)²=b²+c² pelo Teorema de Pitágoras.

Também sabemos que b.c=(2R).h e, portanto, 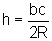. Substituindo, por exemplo, c, obtemos:

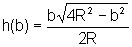, ou seja, a altura escrita em função do cateto b.

Analogamente, podemos escrever h como função do cateto c.

Nesta situação, levando em conta o que estabelecido no exercício anterior, basta observar que e, portanto, elevando ao quadrado e simplificando, temos:

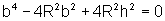
Resolvendo a equação biquadrada,

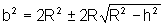
Extraindo a raiz quadrada, obtemos os dois catetos do triângulo. É bom observar que h nunca é maior que R; e se h=R, então o triângulo retângulo é isósceles, ou seja, b=c.

Finalmente então, podemos escrever por exemplo,

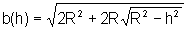
e, nesse caso,