Atrito viscoso num plano inclinado

A seguir veremos um exemplo onde, de uma só vez, aplicamos conceitos de funções, gráficos de funções, escalas (linear e em papel mono-log), reta e equação de regressão através do método dos mínimos quadrados, além de conceitos um pouco mais avançados como equações diferenciais. Ressaltamos, aqui, a importância de conhecermos funções polinomiais do primeiro grau pois, através delas e de uma escala logarítmica, podemos analisar facilmente o comportamento de uma situação, o que seria bastante trabalhoso de ser feito caso usássemos a escala linear. Além disso, é importante também o conceito de derivadas, afinal a aceleração é a derivada da velocidade em relação ao tempo.

Objetivo

Modelar um movimento com atrito viscoso.

Resumo teórico

Suponhamos um corpo deslizando sobre um plano inclinado. Não há atrito entre o corpo e o plano.
O esquema de forças presentes no corpo é mostrado na figura 1.

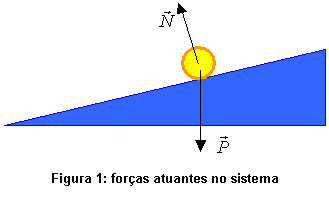
Na figura 1 vemos o peso ( 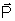) e a força normal ( ). Podemos fazer a decomposição da força peso conforme figura 2:

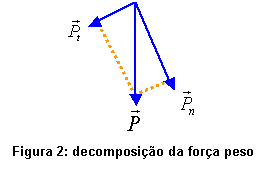
Se o plano forma com a horizontal um ângulo 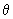, temos que, por semelhança de triângulos, o ângulo entr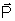e e 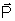_n também será 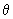. Assim:

A equação do movimento de um corpo nas condições experimentais, ou seja, submetido a uma força externa 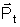constante, num meio viscoso, cuja força viscosa pode ser expressa por 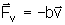é dada por:

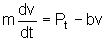,onde b é o coeficiente de atrito (entre o corpo e o ar) (3)

Resolvendo a equação acima obteremos:

Aplicando a condição de contorno v=v₀ para t=0, obtemos:

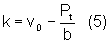
Substituindo (5) em (4) obteremos:

Derivando essa última equação obteremos a aceleração dada por:

(7)

Para a condição inicial em que o corpo parte do repouso (v₀=0) no instante t=0 temos que, em (7), a aceleração inicial é:

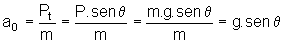(8)

com g=9,7864 m/s² (aceleração da gravidade local).

 

Descrição do experimento

Para a realização dessa experiência, utilizamos um trilho de ar com um desnível entre as extremidades, constituindo um plano inclinado. Na parte mais baixa do trilho, foi conectado um gerador de ar que produz um colchão de ar entre o trilho e o corpo (puque) colocado sobre o trilho. Devido a esse colchão de ar, o movimento ocorre com atrito praticamente desprezível entre o puque e o trilho. A Figura 3 ilustra o experimento.

 

Foi grudada uma fita ao longo do trilho e o puque foi conectado a um faiscador. Ao longo do movimento, o faiscador registrou pontos na fita.

Dados e cálculos

A partir dos dados obtidos, construímos tabelas e gráficos para a dedução das equações que explicam o comportamento do corpo.

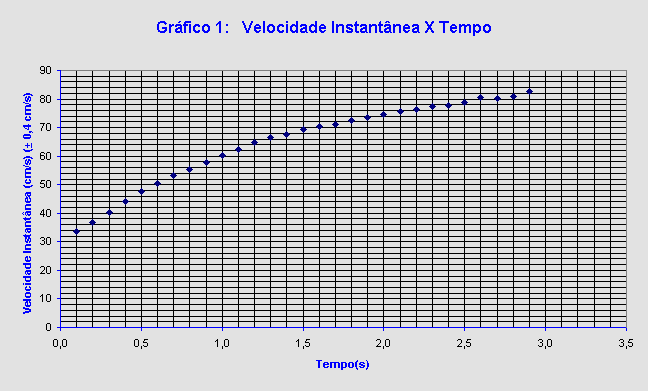
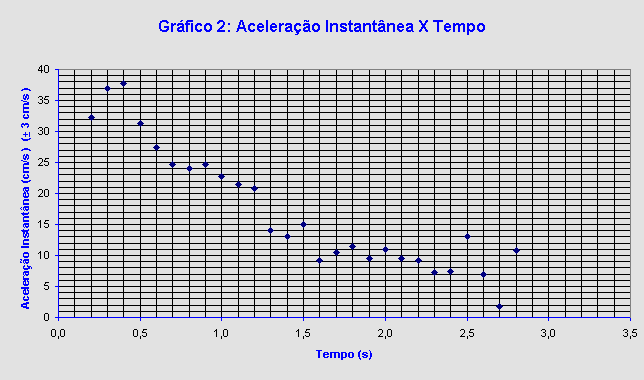
A partir da tabela, construímos os gráficos de velocidade instantânea pelo tempo numa escala linear (Gráfico 1) e da aceleração instantânea pelo tempo (Gráfico 2), ambos numa escala linear .

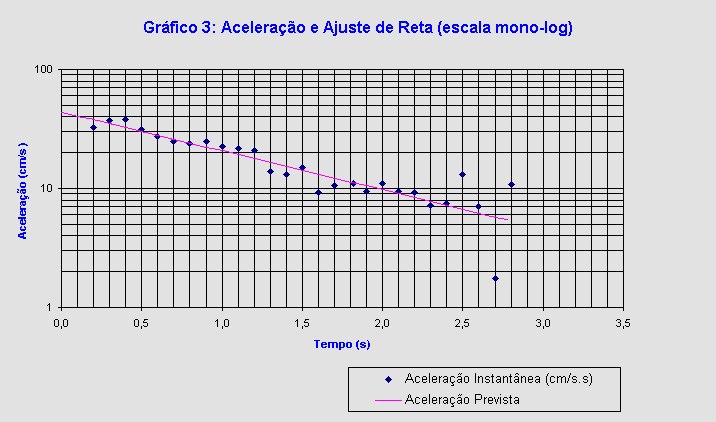
A aceleração instantânea em função do tempo, em escala mono-log, pode ser observada no Gráfico 3, bem como a curva de ajuste. Essa curva foi obtida a partir do método dos mínimos quadrados. Para tal ajuste, calculamos o logaritmo base 10 dos valores observados no experimento.

Nesse ajuste, foram desconsiderados os pontos discrepantes, provavelmente originados devido a algum erro na medida.

A partir do método dos mínimos quadrados, a equação que representa o ajuste da reta é:

a = 43,8 - 0,327.t, (9)

onde a = valor para aceleração instantânea (cm/s²) e t = tempo (em segundos).

A partir da equação (7) podemos deduzir qual a equação do gráfico quando construído no papel mono-log:

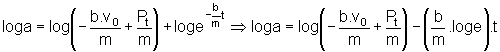(10)

Assim, vemos que o coeficiente angular da reta ajustada (-0,327) corresponde ao termo 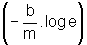, nas equações (9) e (10), respectivamente. A partir disso, e utilizando os dados obtidos do experimento, tais como massa do puque, ângulo do trilho de ar e medições da fita, além de, é claro, as equações deduzidas, podemos calcular todos os demais parâmetros como constantes, velocidades, etc. Isso não poderia ser feito tão facilmente se não utilizássemos uma função do 1º grau.