Algumas funções que podem ser estabelecidas relacionando os elementos de uma figura plana ou espacial 

No contexto da Geometria Euclidiana, existem várias “fórmulas” que permitem o cálculo da área de figuras planas ou o volume de sólidos.

É o caso, por exemplo, da área de um triângulo de base b e altura h, ,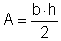

onde b e h são estritamentes positivos.

Evidentemente, a área de um triângulo varia de acordo com as medidas de sua base e
altura. Entretanto, fixada uma dessas medidas, a área do triângulo poderá ser escrita como função apenas da outra medida.

- Assim é que, fixada a altura h, temos:

 

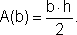
- E também podemos dizer que a medida da base é uma função da área, escrevendo:

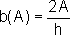
uma vez que a altura está fixa.

Uma outra situação para o estabelecimento de funções é o caso de uma circunferência.

Podemos dizer que:

- O comprimento de uma circunferência é uma função da medida do seu raio:

 

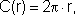
isto é, conforme o raio varia, o comprimento da circunferência varia.


- Também podemos dizer que a área de um círculo é uma função da medida do seu raio:

 

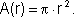
Mas podemos também dizer que a área de um círculo é uma função do comprimento de sua circunferência, escrevendo:

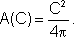
Verifique!

- Analogamente podemos dizer que o comprimento de uma circunferência é uma função da área de seu círculo, escrevendo:

 

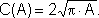
Verifique!

- A área de um círculo é uma função da medida de seu diâmetro, pois:

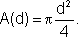
No caso de uma esfera de raio r, temos que seu volume é uma função do raio, segundo a relação:

 

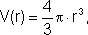
bem como o raio é uma função do volume da esfera, pois:

·       

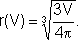Outro exemplo é o caso do cone, onde podemos escrever, por exemplo, que seu volume é uma função da medida do raio da base, uma vez que:

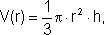
bastando a altura h do cone estar fixada. Mas, se o raio da base r estiver fixado, então podemos encarar o volume do cone como sendo uma função da altura, escrevendo:

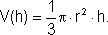
Evidentemente, há uma variedade muito grande de funções que podem ser estabelecidas no âmbito da Geometria, bastando para isso observar que uma das grandezas varia em função de uma outra.