Tomemos como exemplo
a função limitada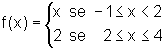 
e
consideremos 
.
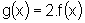Logo,
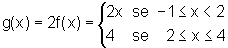
Observando o gráfico de g, temos:
Assim, a função g também é limitada,
pois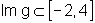 
. Note
que esse intervalo possui 6 unidades de comprimento, o dobro do comprimento
do intervalo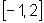 
que contém a imagem de f.
Observação.
Note que se a função inicial tem sua imagem contida num
intervalo [a,b], portanto, de comprimento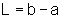 
,
a função obtida através de uma mudança de
inclinação, tem imagem contida num outro intervalo, de comprimento
diferente.
Para qualquer outro
valor de a, a conclusão é semelhante: o gráfico
de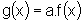 
sofre
uma mudança de inclinação provocada pelo fator a,
quando comparado ao gráfico da função f e,
sendo
f limitada, a função g também é
limitada.
 |
 |