Propriedade: Se f é uma função limitada, então a função 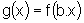também é limitada.

Hipótese: Existe um número real M>0, tal que .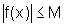

Tese: A função g, tal que 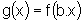, é limitada, isto é existe um número real M₄>0, tal que .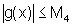

Demonstração:

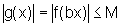
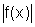
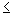
pois 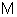, para todo x em seu domínio, por hipótese.

Logo, tomando M₄=M, temos 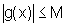, ou seja g é limitada, como queríamos mostrar. Neste caso, o limitante para g é o mesmo que aquele para f.