Atribuindo
valores ao coeficiente a, por exemplo a =
2, a = 3, a = 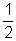 , a =
, a = 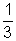 , ou qualquer outro valor positivo, podemos verificar o que acontece.
A seguir, atribuindo valores negativos ao coeficiente a, por exemplo,
a = -1, a = -2,
, ou qualquer outro valor positivo, podemos verificar o que acontece.
A seguir, atribuindo valores negativos ao coeficiente a, por exemplo,
a = -1, a = -2,
a = -3, a
= -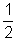 , a = -
, a = -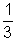 ,
e assim por diante, poderemos chegar a uma conclusão geral.
,
e assim por diante, poderemos chegar a uma conclusão geral.
Observemos, por exemplo,
que no gráfico de 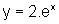 ,
em cada ponto, a ordenada é o dobro daquela do ponto de mesma abscissa
do gráfico de
,
em cada ponto, a ordenada é o dobro daquela do ponto de mesma abscissa
do gráfico de 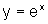 .
Dessa forma, o coeficiente 2 na expressão da função
provoca mudança
de inclinação na curva que é o seu gráfico,
em comparação ao inicial.
.
Dessa forma, o coeficiente 2 na expressão da função
provoca mudança
de inclinação na curva que é o seu gráfico,
em comparação ao inicial.
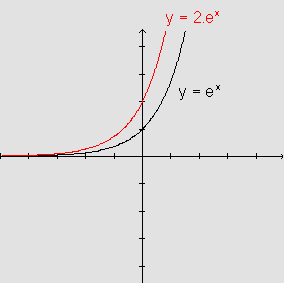
Da mesma forma, fazendo
a = 3, o gráfico de ![]() terá
o triplo da inclinação do gráfico de
terá
o triplo da inclinação do gráfico de 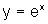 .
.
No caso, por exemplo, de a = 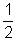 , a =
, a = 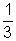 , o ponto do gráfico de
, o ponto do gráfico de ![]() terá
inclinação igual à metade ou à terça
parte, respectivamente, daquela do gráfico de
terá
inclinação igual à metade ou à terça
parte, respectivamente, daquela do gráfico de 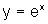 .
.
Graficamente, temos:
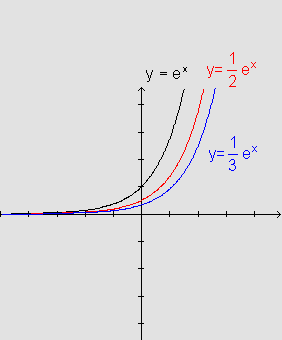
No caso do coeficiente
a ser negativo, observamos inicialmente a situação
mais simples de ![]() .
Cada ponto desse gráfico tem ordenada igual ao oposto do valor
da ordenada do ponto de mesma abscissa em
.
Cada ponto desse gráfico tem ordenada igual ao oposto do valor
da ordenada do ponto de mesma abscissa em 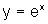 .
O seu gráfico é, portanto, uma curva simétrica,
em relação ao eixo horizontal, à curva que é
o gráfico de
.
O seu gráfico é, portanto, uma curva simétrica,
em relação ao eixo horizontal, à curva que é
o gráfico de 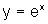 .
.
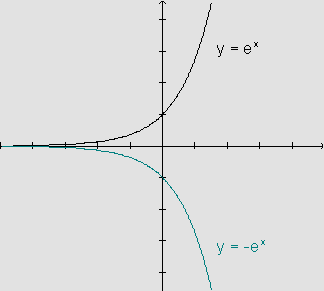
Analogamente, podemos fazer o gráfico considerando qualquer outro valor negativo de a, observando a simetria em relação ao eixo horizontal, quando fazemos a comparação com o gráfico da função oposta.
Assim, o coeficiente
a, em ![]() ,
tem o papel de mudar a inclinação do gráfico da função
,
tem o papel de mudar a inclinação do gráfico da função
![]() .
Quando
.
Quando ![]() ,
a curva tem maior inclinação; quando
,
a curva tem maior inclinação; quando ![]() ,
tem inclinação menor. Quando o coeficiente a é negativo,
o gráfico de
,
tem inclinação menor. Quando o coeficiente a é negativo,
o gráfico de
![]() sofre uma reflexão em relação ao eixo horizontal,
quando comparado ao gráfico da função oposta.
sofre uma reflexão em relação ao eixo horizontal,
quando comparado ao gráfico da função oposta.
