A
fim de entender o que está ocorrendo, vamos atribuir valores à
constante b como, por exemplo, b = 2,
b = 3, 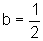 e
e 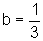 .
.
Nos casos, b
= 2 e b = 3, traçando os gráficos de 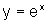 ,
,
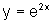 e
e 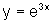 num mesmo par de eixos obtemos:
num mesmo par de eixos obtemos:
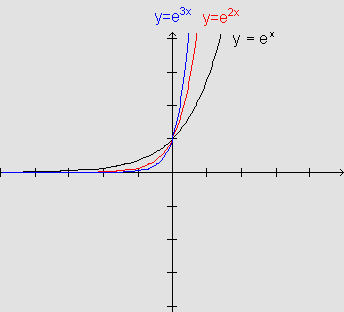
Comparando os três gráficos, observamos que o ponto (0,1)
pertence a todos, embora, em comparação com o gráfico
inicial de 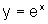 ,
nos outros dois gráficos tenha havido mudança de inclinação.
,
nos outros dois gráficos tenha havido mudança de inclinação.
É interessante observar que 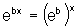 e, portanto o coeficiente b provoca mudança de base na exponencial:
em
e, portanto o coeficiente b provoca mudança de base na exponencial:
em 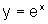 , a base
é e, enquanto que, em
, a base
é e, enquanto que, em 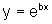 ,
a base é
,
a base é 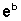 .
.
Assim, comparando
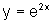 e
e 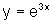 ,
observamos que o gráfico da segunda está acima daquele da
primeira função, para todos os valores da variável
x>0, pois
,
observamos que o gráfico da segunda está acima daquele da
primeira função, para todos os valores da variável
x>0, pois 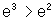 .
.
Por outro lado, para x<0, o gráfico da segunda está abaixo
do gráfico da primeira função, pois 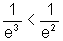 .
.
Já nos casos 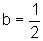 e
e 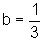 , quando traçamos
num mesmo par de eixos os gráficos de
, quando traçamos
num mesmo par de eixos os gráficos de 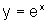 ,
,
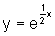 e de
e de 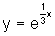 ,
obtemos:
,
obtemos:
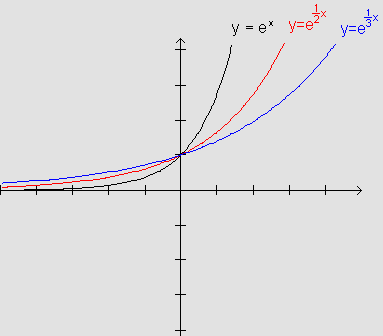
Comparando os três gráficos, observamos que, novamente, o
ponto (0,1) se manteve fixo havendo, em comparação ao gráfico
inicial de 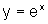 ,
mudança de inclinação nos outros dois gráficos.
,
mudança de inclinação nos outros dois gráficos.
Observando que 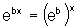 ,
comparando
,
comparando 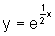 e
e 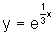 , observamos
que o gráfico da segunda está abaixo do da primeira função,
para todos os valores da variável x>0, pois
, observamos
que o gráfico da segunda está abaixo do da primeira função,
para todos os valores da variável x>0, pois 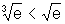 .
.
Por outro lado, para x<0, o gráfico da segunda está acima
do gráfico da primeira função, pois 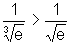 .
.
É necessário considerar também a situação
em que o coeficiente b
é negativo.
Nesse caso, o gráfico
de 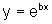 é
o simétrico,
em relação ao eixo vertical, do gráfico de
é
o simétrico,
em relação ao eixo vertical, do gráfico de 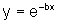 .
.
Por exemplo, colocando
os gráficos de 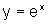 e de
e de 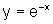 num mesmo
par de eixos, temos:
num mesmo
par de eixos, temos:
observe que, se b<0, então -b>0
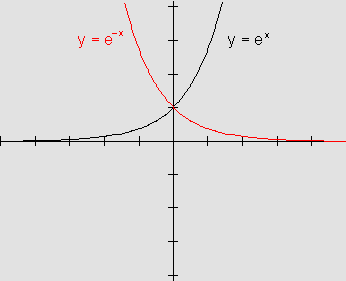
Analogamente, podemos construir o gráfico considerando qualquer outro valor negativo de b, observando a simetria em relação ao eixo vertical, quando fazemos a comparação com o gráfico da função que tem, no expoente, o mesmo coeficiente b em valor absoluto, mas positivo.
