![]() Esboce o gráfico de
Esboce o gráfico de 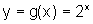 e de
e de 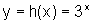 , comparando-os
com o gráfico de
, comparando-os
com o gráfico de 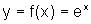 .
.
![]() De modo geral,
De modo geral, 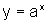 ,
com a>0 e
,
com a>0 e 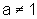 , é
uma função exponencial de base a. Discuta seu gráfico,
comparando-o com o de
, é
uma função exponencial de base a. Discuta seu gráfico,
comparando-o com o de 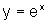 .
.
![]() Considere as funções
Considere as funções 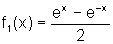 e
e 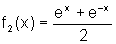 . Mostre que f1
é uma função
ímpar, enquanto que f2 é
uma função par. Mostre também que
. Mostre que f1
é uma função
ímpar, enquanto que f2 é
uma função par. Mostre também que 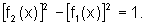
![]() Considere
as duas funções do Exercício 3, e tente esboçar
os seus gráficos, utilizando o fato de serem, respectivamente,
a primeira, par e a segunda, ímpar.
Considere
as duas funções do Exercício 3, e tente esboçar
os seus gráficos, utilizando o fato de serem, respectivamente,
a primeira, par e a segunda, ímpar.
![]() Esboce
o gráfico de cada uma das funções abaixo
Esboce
o gráfico de cada uma das funções abaixo
a) 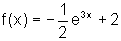
b) 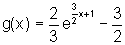
fazendo, para cada uma delas, os gráficos intermediários,
todos num mesmo par de eixos.
![]() Uma população de mosquitos desenvolve-se segundo o modelo
dado pela função:
Uma população de mosquitos desenvolve-se segundo o modelo
dado pela função: 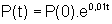 ,
onde a variável t indica o tempo dado em dias. Qual é a
população inicial, sabendo que após 40 dias a população
é de, aproximadamente, 400 000 indivíduos?
,
onde a variável t indica o tempo dado em dias. Qual é a
população inicial, sabendo que após 40 dias a população
é de, aproximadamente, 400 000 indivíduos?
![]() Uma determinada substância radioativa desintegra-se com o tempo,
segundo o modelo dado por m(t) = mo.e-kt, onde m
Uma determinada substância radioativa desintegra-se com o tempo,
segundo o modelo dado por m(t) = mo.e-kt, onde m
Observação: a meia-vida de uma substância radioativa
é o tempo necessário para que a massa inicial fique reduzida
à metade.
![]() Sabendo que 100g de Tório diminuem para 75g em 33600 anos, calcule
em quanto tempo 100g se reduzem a 90g.
Sabendo que 100g de Tório diminuem para 75g em 33600 anos, calcule
em quanto tempo 100g se reduzem a 90g.
![]() Resolva a equação exponencial:
Resolva a equação exponencial: 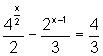 .
.
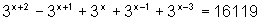 .
.