Sendo g(x)=2x+1 e f(x)=(2x+1)², podemos observar o que está acontecendo através de um diagrama.

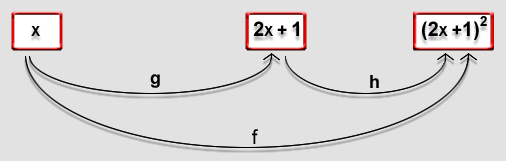
Podemos considerar, examinando o esquema acima, que temos uma função f(x)=(2x+1)² que a cada valor de x associa o valor (2x+1)².

Por outro lado, verificamos que cada valor da variável x é levado, pela função g, num valor g(x)=2x+1 que, por sua vez, é levado num outro valor que é (2x+1)². Podemos imaginar que nessa segunda etapa está presente uma outra função h, que, a cada valor da variável independente associa o seu quadrado, ou seja, h(u)=u².

Evidentemente, poderíamos ter considerado a função f(x)=(2x+1)², que, a cada valor de x associa diretamente o valor (2x+1)².

Dizemos, nesse caso, que a função f foi obtida pela composição de h com g e escrevemos f(x)=h(g(x)), querendo exprimir o fato de que x sofre inicialmente a ação de g e, em seguida, a ação de h.

A partir das funções originais g e h, a função f também pode ser denotada segundo a notação:

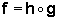
onde queremos dizer que, para todo x, 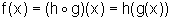.