![]()
Dadas
as funções g(x)=x+1, com Dom g=R e Im g=R, e h(x)=x-1, com
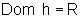 e Im h=R, então
e Im h=R, então
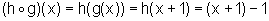
Logo
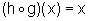 ,
com Dom
,
com Dom 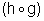 =R e Im
=R e Im
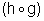 =R.
=R.
Devemos observar que
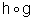 existe para todo
x real, pois a composição é sempre possível,
uma vez que
existe para todo
x real, pois a composição é sempre possível,
uma vez que 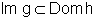 - na verdade,
nesse caso são ambos iguais a R.
- na verdade,
nesse caso são ambos iguais a R.
Por outro lado,
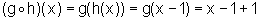
Então
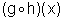 =x,
com Dom
=x,
com Dom 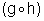 =R e Im
=R e Im
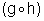 =R.
=R.
Novamente devemos
observar que 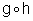 existe
para todo x real, pois a composição é sempre possível,
uma vez que
existe
para todo x real, pois a composição é sempre possível,
uma vez que 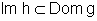 - na
verdade, nesse caso também são ambos iguais a R.
- na
verdade, nesse caso também são ambos iguais a R.
Nesse exemplo, as
funções g e h são inversas,
pois
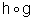 =
= 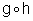 =Id,
onde Id é a função identidade, Id(x)=x, para todo
x real.
=Id,
onde Id é a função identidade, Id(x)=x, para todo
x real.
 |
