Estamos olhando um subconjunto de sucessivos naturais que, no enunciado do teorema, começa em n=1.
Se esse conjunto começar, por exemplo, em n=500 então o Teorema é o seguinte:
Seja P(n) uma propriedade descrita em termos de números naturais n. Suponhamos que as afirmações abaixo estejam satisfeitas:
a) P(500) é
válida.
b) Se P(k-1) vale então P(k) também
vale.
Nesse caso então
P(n) é válida para todo 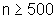 .
.
Note que, nesse caso, o Princípio da Indução Finita não garante a validade da afirmação P(n) para n<500.
