Alguns dados históricos

Desde os tempos de Euclides, os matemáticos utilizaram durante séculos, o princípio da indução sem, entretanto, dar-lhe um nome específico. Talvez isto se devesse ao fato de que ainda não tivessem noção das peculiaridades desta maneira de demonstrar fatos, bem como de sua fecundidade. Mesmo quando essa consciência começou a se tornar explícita, como em F. Maurolico (1494-1575) e em B. Pascal (1623-1662), o raciocínio indutivo continuou sem um nome que o caracterizasse.

O primeiro matemático que utilizou o termo "indução", para indicar uma forma de demonstrar teoremas, foi J. Wallis (1617-1703) em sua obra Arithmetica Infinitorum, publicada em 1656. Entretanto, para ele, a indução é aquela das ciências experimentais, e não a indução matemática.

A expressão "indução matemática", para indicar o raciocínio que permite passar de n a n+1, foi criada pelo matemático inglês A. De Morgan (1808-1871), em seu artigo Induction (Mathematics), publicado em 1838, na Penny Cyclopedia.

Tal expressão não teve uma difusão imediata. O matemático alemão H. Grassmann (1809-1877), em seu Tratado de Aritmética de 1861, utiliza fortemente a indução matemática para definir as operações aritméticas e para demonstrar suas propriedades, sem contudo nomeá-la dessa maneira; ela é apresentada apenas como um "raciocínio conhecido", tranqüilamente aceito pelos matemáticos.

A expressão "indução completa" foi inventada por R. Dedekind (1831-1916), que a utilizou em sua obra Was sind und was sollen die Zahlen, publicada em 1887. Nessa mesma obra, Dedekind utiliza, como sinônimo para "método de indução", a expressão "argumentação recorrente" e, como sinônimo de "definição indutiva", a expressão "definição por recorrência". Essas duas últimas expressões foram também as escolhidas por H. Poincaré (1854-1912).

G. Peano (1858-1932), matemático italiano, foi o primeiro que deu uma construção axiomática da aritmética em 1889, em sua obra Arithmetices principia novo methodo exposita. Boyer, em sua História da Matemática, relata: "Os axiomas de Peano representaram a tentativa mais singular, realizada no século XIX, de reduzir a aritmética comum e, conseqüentemente, a maior parte da matemática, à pura essência do simbolismo formal. O método axiomático alcançou um tal grau de precisão nunca antes alcançado, não dando margem a ambigüidades ou a suposições tácitas".

A formulação de Peano é a seguinte:

Seja A um conjunto de números naturais e dado um natural n, indiquemos por S(n) seu sucessor. Se:

• ;
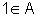• para cada número natural n, se 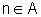, também ,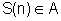

então A=N, isto é, A é o conjunto de todos os naturais.

Utiliza-se também uma formulação em termos de propriedades, da seguinte maneira:

Para cada número natural n, consideremos a propriedade P_n. Se:

• P1 é verdadeira, isto é, vale P_n para n=1;
• para todo natural r, do fato de P_n ser verdadeira para n=r, pode-se deduzir que P_n é verdadeira para n=S(r),

então P_n é verdadeira para todo número natural n.