Suponha que uma proposição P(n) tenha as seguintes propriedades:

• P(4) vale;
• Se P(k) vale então P(k+1) também vale.

Então, P(n) vale para todo .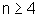

Vamos provar que 2ⁿ>3.n, para todo .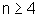

Em primeiro lugar, escrevemos P(4): 2⁴ >3.4 que é verdadeira pois 16>12.

Suponhamos agora que vale P(k): 2^k >3.k.

E vamos provar que, então, vale P(k+1), isto é, 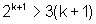. Temos:

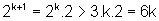
Observemos que 6k=3k+3+3k-3=3(k+1)+3(k-1)>3(k+1), pois k 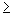4.

Logo, .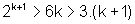

ou seja, vale P(k+1).

E portanto, pelo P.I.F., P(n) é válida para todo 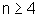.