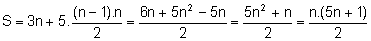a) S=2+4+6+...+2n

Primeiramente, observemos que S pode ser escrito de outra maneira:

S=2.(1+2+3+....+n)= ,

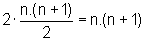pois utilizamos a Situação 1. Logo, S=n.(n+1).

b) S=3+8+13+...+(5n-2)

A seqüência é uma Progressão Aritmética, cuja razão entre quaisquer dois termos é 5.

Por outro lado, observamos que cada termo é, sucessivamente, a soma de 3 com um múltiplo de 5. Logo, a soma procurada pode ser escrita da seguinte maneira:

S=3+(3+5.1)+(3+5.2)+(3+5.3)+...+[3+5.(n-1)]

ou seja,

S=3n+5.(1+2+3+...+(n-1))

Logo, pela Situação 1,