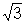 é um número irracional.
é um número irracional.
De fato, se 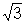 não fosse um número irracional, então
não fosse um número irracional, então 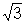 poderia ser escrito na forma de uma fração, onde numerador
e denominador são inteiros e o denominador é não
nulo, ou seja:
poderia ser escrito na forma de uma fração, onde numerador
e denominador são inteiros e o denominador é não
nulo, ou seja:
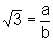 onde
onde 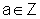 e
e 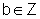 ,
,
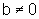 .
.
Suponhamos que a fração está escrita na forma irredutível, isto é, a e b são primos entre si.
Então,
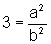 ou seja,
ou seja, 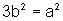
isto é, 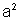 é um número múltiplo de 3. Logo,
a é também múltiplo de 3.
é um número múltiplo de 3. Logo,
a é também múltiplo de 3.
Ou seja, a=3k,  .
.
Então, podemos
escrever: 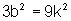 ou
ou  ,
,
de onde temos 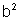 que é um número múltiplo de 3. Logo, b é
também múltiplo de 3.
que é um número múltiplo de 3. Logo, b é
também múltiplo de 3.
Mas, a ser
múltiplo de 3 e b ser múltiplo de 3 contradiz a hipótese
de que a e b sejam primos entre si, ou seja, temos um absurdo.
Portanto, 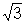 é um número irracional, como queríamos provar.
é um número irracional, como queríamos provar.
