A tabela-verdade para o " 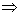" (implicação) é a seguinte:
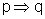V
V
V
V
F
F
F
V
V
F
F
V


Isso significa que, a implicação só é F quando temos uma proposição V acarretando uma proposição F. Assim se, a partir de uma asserção verdadeira pretendermos concluir outra asserção que é falsa, nossa pretensão é falsa.

Por outro lado, se, a partir de uma asserção verdadeira pretendermos concluir outra asserção que é verdadeira, nossa pretensão é verdadeira.

Finalmente, se, a partir de uma asserção falsa pretendermos concluir outra asserção que é verdadeira ou falsa, nossa pretensão é verdadeira.

Na proposição 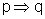, a frase p é chamada hipótese e a frase q é denominada tese.

Por exemplo, sendo x um número inteiro qualquer, temos que:

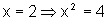
Notemos que de 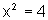não podemos tirar a conclusão de que x=2. Poderíamos ter 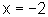. Assim, 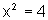não implica que .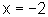

Outro exemplo: se uma pessoa é paulista, isso implica que ela é brasileira. Mas, do fato de uma pessoa ser brasileira não podemos concluir que ela é paulista. Ela poderia ser carioca, gaúcha, e assim por diante.

O que podemos afirmar é que se ela não é brasileira, então não pode ser paulista.

De modo geral, 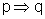é o mesmo que 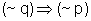. Para mostrar esse fato, basta mostrar que a tabela-verdade de 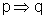e a de coincidem. De fato,
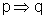V
V
V
F
F
V
V
F
F
V
F
F
F
V
V
F
V
V
F
F
V
V
V
V

Este fato é importante, por ser bastante utilizado em demonstrações. Quando pretendemos mostrar que 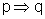, muitas vezes, fazemos a demonstração por absurdo, ou seja, negamos a tese e passamos a fazer a demonstração de que . Como essa nova implicação acarreta na negação de p, sendo que p é a hipótese inicial, chegamos a uma contradição, ou absurdo, de onde concluímos que a proposição 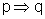é verdadeira.

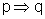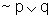Outro fato importante é que a proposição é equivalente à proposição . Para mostrar esse fato, basta examinar a tabela-verdade de cada uma delas e verificar que elas coincidem. Com efeito,
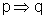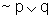V
V
V
F
V
V
F
F
F
F
F
V
V
V
V
F
F
V
V
V


É importante saber que existem diversos modos de dizer: se p, então q.