A tabela-verdade
para a "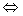 
"
(equivalência) é a seguinte:
 |
 |
 |
|
V
|
V
|
V
|
|
V
|
F
|
F
|
|
F
|
V
|
F
|
|
F
|
F
|
V
|
Isso significa que, a dupla-implicação só é
V quando as proposições iniciais são ambas V ou ambas
F. E, por outro lado a dupla-implicação só é
F quando temos uma proposição V acarretando uma proposição
F, ou vice-versa.
Por exemplo, sendo
x um número inteiro qualquer, temos que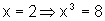 
.
Assim, 
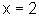implica que 
.
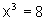Notemos que de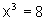
podemos tirar a conclusão de que x=2. Assim,
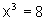implica que 
.
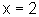S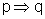e 
e 
,
então temos uma equivalência e podemos escrever 
.
No caso acima,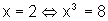 
.
Quando resolvemos equações, devemos tomar cuidado ao realizar operações em ambos os membros, para que a nova equação seja equivalente à anterior, pois, senão houver equivalência, o conjunto solução encontrado não será necessariamente o conjunto solução da equação inicial. É o caso, por exemplo, de elevar ao quadrado os dois membros da equação.
A proposição
é
equivalente à proposição 
.
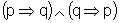Vamos mostrar esse fato através das tabelas-verdade.
|
|
|
|
 |
 |
 |
|
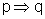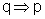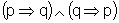V
|
V
|
V
|
V
|
V
|
V
|
|
V
|
F
|
F
|
F
|
V
|
F
|
|
F
|
V
|
F
|
V
|
F
|
F
|
|
F
|
F
|
V
|
V
|
V
|
V
|
É importante saber que existem diversos modos de dizer: se p, então q, e vice-versa.
 |
 |