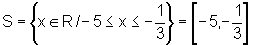A tabela-verdade
para o " 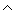 " (e) é a seguinte:
" (e) é a seguinte:
|
p
|
q
|
 |
|
V
|
V
|
V
|
|
V
|
F
|
F
|
|
F
|
V
|
F
|
|
F
|
F
|
F
|
Isso significa que, se pelo menos uma das proposições básicas
dadas é falsa, a proposição  é falsa. Assim, o conectivo e é colocado quando se
pretende que ambas as condições descritas nas proposições
iniciais sejam verificadas.
é falsa. Assim, o conectivo e é colocado quando se
pretende que ambas as condições descritas nas proposições
iniciais sejam verificadas.
Por exemplo, sejam as proposições:
p: Todas as pessoas
com idade superior a 30 anos.
q: Todas as pessoas que estudam na USP.
A proposição
 é então:
"todas as pessoas com idade superior a 30 anos e que estudam na USP".
Essa proposição refere-se a um conjunto de pessoas que estudam
na USP e que, ao mesmo tempo, têm mais do que 30 anos. Para uma
pessoa estar nesse conjunto - isto é, a frase
é então:
"todas as pessoas com idade superior a 30 anos e que estudam na USP".
Essa proposição refere-se a um conjunto de pessoas que estudam
na USP e que, ao mesmo tempo, têm mais do que 30 anos. Para uma
pessoa estar nesse conjunto - isto é, a frase  é verdadeira para ela - é preciso que ela satisfaça
as duas condições dadas pelas frases inicialmente propostas
- ou seja, ambas as frases p e q são verdadeiras.
é verdadeira para ela - é preciso que ela satisfaça
as duas condições dadas pelas frases inicialmente propostas
- ou seja, ambas as frases p e q são verdadeiras.
De modo geral,  é o mesmo que
é o mesmo que 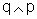 .
Para provar esse fato, basta mostrar que a tabela-verdade de
.
Para provar esse fato, basta mostrar que a tabela-verdade de  e a de
e a de 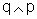 coincidem.
De fato,
coincidem.
De fato,
|
p
|
q
|
 |
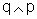 |
|
V
|
V
|
V
|
V
|
|
V
|
F
|
F
|
F
|
|
F
|
V
|
F
|
F
|
|
F
|
F
|
F
|
F
|
Outro fato que pode ser apresentado é que, dadas duas proposições
p e q, a negação da proposição
 pode ser obtida
a partir das negações ~p e ~q. Nesse caso, através
da tabela-verdade, podemos mostrar que a negação da conjunção
é a disjunção
das negações, ou seja:
pode ser obtida
a partir das negações ~p e ~q. Nesse caso, através
da tabela-verdade, podemos mostrar que a negação da conjunção
é a disjunção
das negações, ou seja: 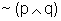 equivale a
equivale a 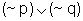 .
Com efeito,
.
Com efeito,
|
p
|
q
|
 |
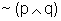 |
~p
|
~q
|
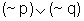 |
|
V
|
V
|
V
|
F
|
F
|
F
|
F
|
|
V
|
F
|
F
|
V
|
F
|
V
|
V
|
|
F
|
V
|
F
|
V
|
V
|
F
|
V
|
|
F
|
F
|
F
|
V
|
V
|
V
|
V
|
Uma situação em que aparece a questão da conjunção
de duas proposições pode ser, por exemplo, a resolução
de um sistema de duas inequações onde cada inequação
é uma proposição. Quando procuramos a solução
do sistema, procuramos o conjunto de números que satisfazem, isto
é, tornam verdadeiras, ambas as inequações.
Um sistema simples poderia ser:
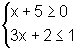
onde a primeira inequação
é verdadeira para 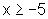 ,
enquanto que a segunda é verdadeira para
,
enquanto que a segunda é verdadeira para 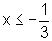 .
.
Logo a solução do sistema é dada por: