Dadas as afirmações:
(I) Se um político
tem muito dinheiro, então ele pode ganhar as eleições.
(II) Se um político não tem muito dinheiro, então
ele não pode ganhar as eleições.
(III) Se um político pode ganhar as eleições, então
ele tem muito dinheiro.
(IV) Se um político não pode ganhar as eleições,
então ele não tem muito dinheiro.
(V) Um político não pode ganhar as eleições,
se ele não tem muito dinheiro.
Sejam:
p: Um político
tem muito dinheiro;
q: Ele pode ganhar as eleições.
As afirmações dadas podem ser então escritas na maneira seguinte:
(I)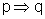 
(II)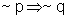 
(III)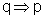 
(IV)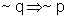 
(V)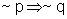 
a) Assumindo que (I) é verdadeira, apenas a afirmação (IV) é verdadeira.
Para verificar esse fato, vamos examinar as tabelas-verdade:
|
p
|
q
|
~p
|
~q
|
 |
 |
 |
 |
 |
|
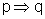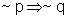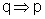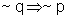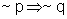V
|
V
|
F
|
F
|
V
|
V
|
V
|
V
|
V
|
|
V
|
F
|
F
|
V
|
F
|
V
|
V
|
F
|
V
|
|
F
|
V
|
V
|
F
|
V
|
F
|
F
|
V
|
F
|
|
F
|
F
|
V
|
V
|
V
|
V
|
V
|
V
|
V
|
Observe que as duas únicas colunas iguais são aquelas em
vermelho.
b) A negação
de (I) é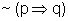 
:
"Não é verdade que se um político tem muito
dinheiro então ele pode ganhar as eleições".
Podemos observar essa
resolução com um pouco mais de detalhe.
Vejamos: a afirmação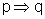 
é equivalente
a 
.
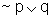Logo, a afirmação
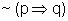é equivalente
a 
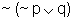que, por
sua vez, é equivalente a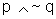 
.
Vamos verificar essa última equivalência através da
tabela-verdade:
|
p
|
q
|
~p
|
~q
|
 |
 |
 |
|
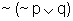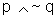V
|
V
|
F
|
F
|
V
|
F
|
F
|
|
V
|
F
|
F
|
V
|
F
|
V
|
V
|
|
F
|
V
|
V
|
F
|
V
|
F
|
F
|
|
F
|
F
|
V
|
V
|
V
|
F
|
F
|
Logo a equivalência entr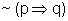e 
e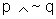 
nos permite
dizer que:
"Existe um político que tem muito dinheiro e que não
ganha as eleições".
c) A afirmação
recíproca de (I), 
,
é a seguinte:
Se ele pode ganhar as eleições, então ele tem muito
dinheiro.
d) A afirmação
contra-positiva de (I),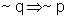 
,
é a seguinte:
Se ele não pode ganhar as eleições, então
ele não tem muito dinheiro.
 |
 |