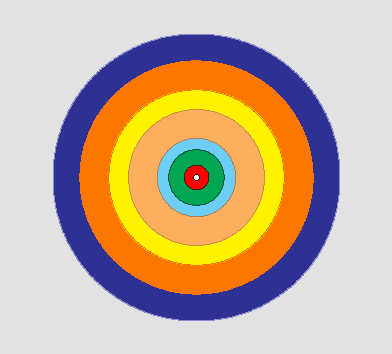
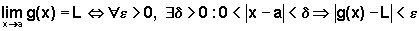Num jogo de lançamento de dardos, você tem um tabuleiro constituído de uma série de circunferências concêntricas:

Para obter pontuação máxima, é preciso acertar no centro. Entretanto, se você permitir certa margem de erro, poderá ao lançar o dardo, atingir algum ponto do tabuleiro, mesmo fora do centro, e obter alguma pontuação.

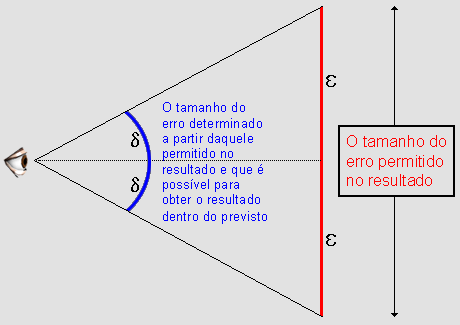
Suponhamos então que o resultado do lançamento dependa do ângulo entre a horizontal - que liga o ponto de lançamento ao centro do tabuleiro - e uma reta imaginária que liga o ponto de lançamento ao ponto atingido. Sabendo qual sua margem de erro (e) para obter alguma pontuação, você tem uma variação delimitada (d) para o referido ângulo.

Vamos precisar estabelecer uma certa formalização a fim de tratar das questões de limites com algum rigor. Com efeito, os conceitos de derivada e de integral são construídos como um determinado limite e, para desenvolver completamente esses conceitos fundamentais no Cálculo, precisamos da definição rigorosa de limite.

Observamos que, ao dizer que 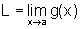, estamos lidando com aproximações pois estamos dizendo que, conforme x se aproxima de a, o valor de g(x) se aproxima de L.

Por exemplo, ao dizer que 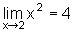, estamos dizendo que conforme x se aproxima de 2, o valor x² se aproxima de 4.

A questão é: como se relacionam essas aproximações?

Como no exemplo do lançamento do dardo, precisamos ter controle sobre o erro que pode ser cometido pelo valor da variável independente x quando pretendemos que o resultado g(x) esteja próximo de L.

Isso significa que a situação pode ser descrita da seguinte maneira: sabendo de quanto nos permitimos errar no resultado da variável dependente, perto do limite L, queremos saber de quanto podemos errar na variável independente x, a fim de cairmos na margem de erro permitida inicialmente.

Ou seja: dizemos que 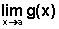=L, quando, estabelecido o erro permitido na variável dependente, conseguimos encontrar qual o erro que podemos cometer na variável independente, a fim de que com esse erro, o valor de y=g(x) fique dentro da margem de erro pré-estabelecida.

Vamos construir uma tabela para deixar clara a idéia envolvida, no caso de :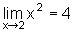

Erro permitido no cálculo do limite: e	intervalo onde g(x) pode estar	Intervalo onde x tem que estar (x 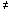2)	Erro permitido na variável x: d
0,1	3,9< g(x)< 4,1	1,97<x<2,02	0,02
0,01	3,99< g(x)< 4,01	1,997<x<2,002	0,002
0,001	3,999<g(x)< 4,001	1,9997<x<2,0002	0,0002
0,0001	3,9999<g(x)< 4,0001	1,99997<x<2,00002	0,00002

É claro que poderíamos continuar a tabela indefinidamente...

Entretanto, o que deve estar claro é que, para cada valor de x no intervalo encontrado, o valor da função g(x) nesse ponto estará dentro da limitação escolhida, ou permitida, inicialmente. Também é preciso observar que, como o intervalo encontrado não é simétrico em relação a 2, escolhemos o maior intervalo simétrico aí contido.

Assim, ao cometermos um erro na variável x, menor do que o tamanho encontrado, estaremos, certamente, cometendo um erro, quando calcularmos o valor da função nesse ponto escolhido, menor do que o permitido, em relação ao valor do limite.

De modo geral, dizer qu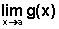e =L é equivalente a dizer que: para todo erro de tamanho e >0, existe um erro de tamanho d >0, tal que, se o valor da variável independente x - diferente de a - está próximo de a, a menos de d, o valor da variável dependente y=g(x) estará próximo de L, a menos de e .

Equivalentemente, podemos escrever em linguagem simbólica: