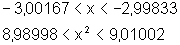Para entender porque 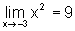, em primeiro lugar observemos que este resultado é razoável. Com efeito, a função f(x)=x² tem domínio real e, portanto está definida no ponto -3.

Em termos de cálculos aproximados, temos que, permitindo um erro de amplitude
e >0, ao redor de L=9, encontramos um erro de amplitude d >0, ao redor de x=-3, de modo que

se 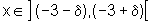então o valor da função .

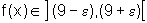Vamos achar o erro d em função do erro que foi dado. Temos:

Algebricamente, temos que é dado e >0 tal que .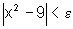

Logo,

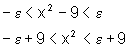
e, portanto, como x é negativo, já que está próximo de -3, temos:

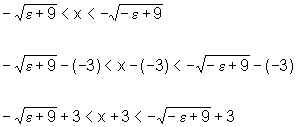
ou seja,

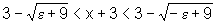
Isso significa que tomando

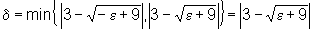
podemos escrever:

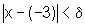ou seja,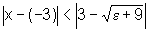

Encontramos assim, a variação permitida para x: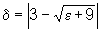 , a fim de não ultrapassar o erro permitido e, que foi dado inicialmente.

Por exemplo, dado e=0,1, pelo cálculo feito, encontramos d=0,00167.

Então, se x está próximo de -3, a menos de 0,00167, isto é, 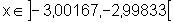então 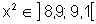. De fato,