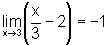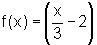Para entender porque , em primeiro lugar observemos que este resultado é razoável. Com efeito, a função tem domínio real e, portanto está definida no ponto 3.

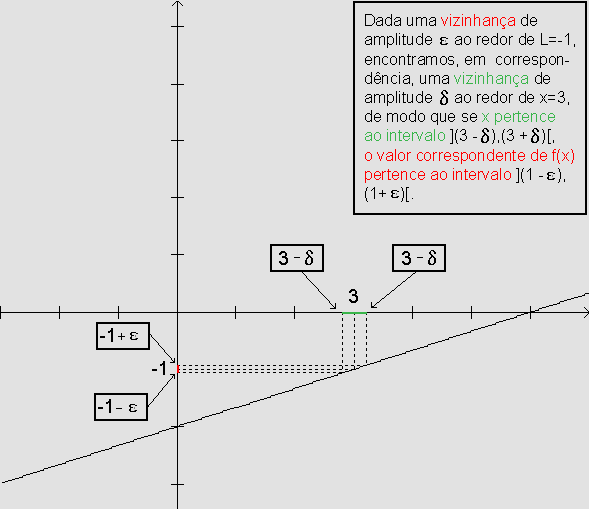
Em termos de cálculos aproximados, temos que, permitindo um erro de amplitude
e >0, ao redor de L= -1, encontramos um erro de amplitude d >0, ao redor de x=3, de modo que:

se 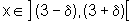então o valor da função .

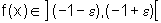Vamos achar o erro d em função do erro e que foi dado. Temos:

Algebricamente, temos:

É dado e >0 tal que 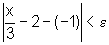, ou seja,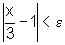

Logo,

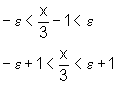
e, portanto,

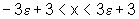
ou seja,

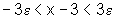isto é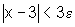

Encontramos assim, a variação permitida para x: d = 3e, a fim de não ultrapassar o erro permitido e, que foi dado inicialmente.

Por exemplo, dado e =0,03, pelo cálculo feito, encontramos d =0,09.

Então, se x está próximo de 3, a menos de 0,09, isto é, 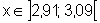então:

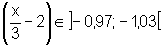
De fato,

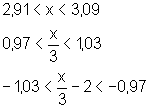
conforme o previsto.