Segunda Regra de L'Hospital

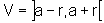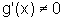Sejam f e g duas funções deriváveis em todo ponto x distinto de a, x pertencente a uma vizinhança V de a, , r>0. Suponhamos que para todo 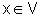e que

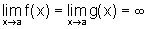
Se existe 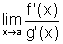, finito ou infinito, então existe 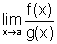e, mais ainda, .

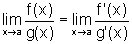Prova:

Sejam x e c dois pontos arbitrários de V, de modo que 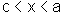ou .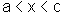

Pelo teorema de Cauchy, temos:

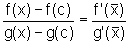, onde .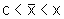

Daí,

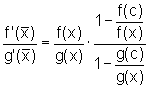
ou

.

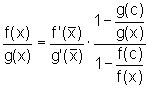Calculando o limite quando e usando a hipótese 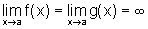, temos:

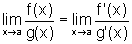
como queríamos provar.

Observações:

1. Se 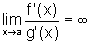ainda temos a mesma conclusão.

De fato, nesse caso, 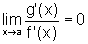e, aplicando a Segunda Regra de L'Hospital, obtemos , de onde .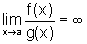

2. O Teorema 2 continua válido no caso em que 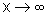ou .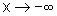

Para verificar esse fato, basta fazer a mudança de variável como na Observação 3 da Primeira Regra de L'Hospital.