A fim de provar o Teorema 1, isto é, a Primeira
Regra de L'Hospital, vamos primeiramente examinar uma outra Propriedade
cujo resultado será usado na demonstração da referida
Regra. Essa propriedade é devida a Cauchy.
Precisamente, temos:
Teorema de Cauchy:
Sejam f e g duas funções contínuas em [a,b], deriváveis
em ]a,b[, tais que 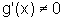 para todo
para todo 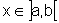 .
Existe então
.
Existe então 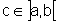 tal que
tal que
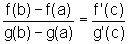
Prova:
Seja 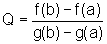 ,
e observemos que
,
e observemos que 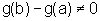 pois se assim não fosse, pelo Teorema
do Valor Médio aplicado à função g,
teríamos que existe
pois se assim não fosse, pelo Teorema
do Valor Médio aplicado à função g,
teríamos que existe 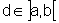 tal que
tal que 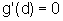 ,
o que é impossível pela hipótese:
,
o que é impossível pela hipótese:  para todo
para todo 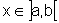 .
.
Consideremos agora uma função F, tal que:
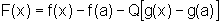 .
.
Temos, substituindo
x por a, 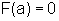 e, substituindo x por b, F(b)=0.
e, substituindo x por b, F(b)=0.
Também, a função
F satisfaz
as hipóteses do TVM e, portanto, existe 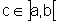 tal que
tal que 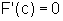 .
.
Por outro lado, achando F' através da expressão de F, temos:
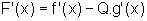
ou seja, 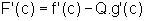 .
.
Como 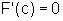 ,
obtemos
,
obtemos 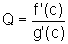 ,
como queríamos provar.
,
como queríamos provar.
Vejamos agora:
Teorema 1: Primeira Regra de L'Hospital
Sejam f e g duas funções
contínuas em um intervalo I, deriváveis no interior
de I, tais que 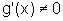 para todo x no interior de I. Seja
para todo x no interior de I. Seja 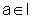 e suponhamos que
e suponhamos que 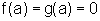 e que existe
e que existe 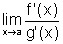 ,
finito ou infinito. Então existe
,
finito ou infinito. Então existe 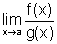 e, mais ainda,
e, mais ainda, 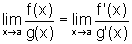 .
.
Prova:
Seja 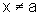 um ponto arbitrário do intervalo I.
um ponto arbitrário do intervalo I.
Aplicando o Teorema
de Cauchy, temos: 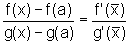 para algum
para algum 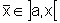 .
.
Como 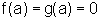 ,
por hipótese, temos:
,
por hipótese, temos:
 (1)
(1)
Agora, 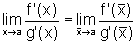
e, de (1) 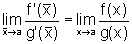
Logo, 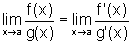
como queríamos provar.
Observações:
1. O Teorema 1 ainda
é verdadeiro no caso em que f e g são deriváveis
em 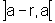 e em
e em 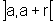 onde r>0, não estando definidas no ponto a, mas com
onde r>0, não estando definidas no ponto a, mas com 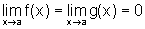 .
.
De fato, basta considerar as funções:
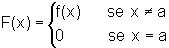
e
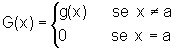
que são contínuas em x=a e observar que:
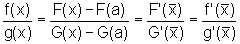 ,
com
,
com 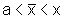 .
.
2. Se 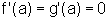 e as funções f' e g' verificam as hipóteses do Teorema,
podemos aplicar novamente a Regra de L'Hospital, obtendo:
e as funções f' e g' verificam as hipóteses do Teorema,
podemos aplicar novamente a Regra de L'Hospital, obtendo:
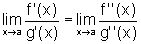
e esse raciocínio pode ser repetido.
3. A Regra de L'Hospital continua válida no
caso em que no lugar de a tivermos 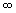 ,
isto é
,
isto é 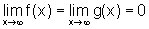 .
.
De fato, basta fazer
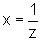 ;
se
;
se 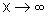 então
então 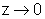 .
Então:
.
Então:
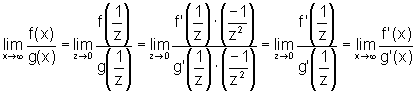 .
.
