Para calcular 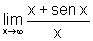 ,
observamos que:
,
observamos que:
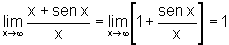
pois
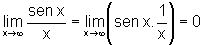 , uma vez
que temos o produto de uma função
limitada por uma que tende a zero.
, uma vez
que temos o produto de uma função
limitada por uma que tende a zero.
Entretanto, o limite do quociente das derivadas das duas funções do numerador e denominador é o seguinte:
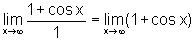 que não existe.
que não existe.
Assim, não
vale a recíproca da Regra de L'Hospital, pois pode acontecer
de existir o 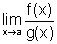 e de não ser igual ao
e de não ser igual ao 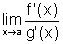 .
.
