![]()
Em primeiro lugar,
observemos que, para 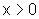 ,
,
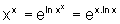
pois a função logarítmica e a função exponencial são inversas.
Assim,
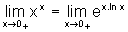 .
.
A fim de calcular
esse limite, vamos antes calcular 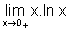 .
.
Temos então:
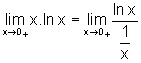 ,
,
onde observamos que ambas as funções no numerador e no denominador satisfazem as hipóteses do Teorema 2. Assim, calculando o limite do quociente das derivadas, temos:
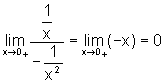 .
.
Logo, pela Regra de L'Hospital,
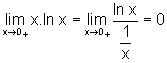 .
.
Voltando ao limite inicial e observando que a função exponencial é uma função contínua, temos que:
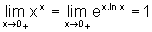 .
.
