No cálculo
de limites nos defrontamos diversas vezes com alguns limites do tipo 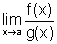 com
com 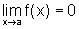 e
e 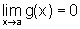 ou então
ou então 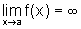 e
e 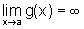 ,
sendo g uma função não identicamente nula
e a um número real, podendo ser
,
sendo g uma função não identicamente nula
e a um número real, podendo ser 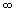 ou
ou 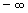 .
.
Nesses exemplos usamos algum tipo de artifício a fim de "sair
da indeterminação" do tipo 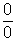 ou
ou  .
Entretanto, por exemplo, em
.
Entretanto, por exemplo, em 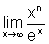 nenhum dos artifícios
vistos no cálculo de limites resolve o problema.
nenhum dos artifícios
vistos no cálculo de limites resolve o problema.
Coube a Bernoulli - embora a publicação tenha sido de L'Hospital, que emprestou seu nome ao feito - descobrir uma propriedade que nos permite calcular rapidamente limites desse tipo. A engenhosa descoberta consistiu em perceber que, na vizinhança de um ponto podemos comparar o quociente de duas funções com o quociente de suas derivadas, desde que determinadas hipóteses estejam satisfeitas. De maneira precisa, temos:
Sejam f e g duas funções contínuas num intervalo
I, deriváveis no interior de I, tais que 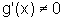 para todo x no interior de I. Seja
para todo x no interior de I. Seja 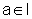 e suponhamos que
e suponhamos que 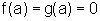 e que existe
e que existe 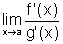 ,
finito ou infinito. Então existe
,
finito ou infinito. Então existe 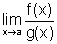 e mais ainda
e mais ainda 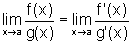 .
.
Sejam f e g duas funções
deriváveis em todo ponto x distinto de a, x pertencente a uma vizinhança
V de a, 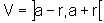 , r>0. Suponhamos que
, r>0. Suponhamos que 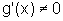 para todo
para todo 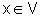 e que
e que 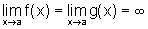 .
Se existe
.
Se existe 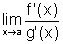 ,
finito ou infinito, então existe
,
finito ou infinito, então existe 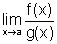 e, mais ainda,
e, mais ainda, 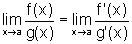 .
.
Com as Regras de L'Hospital muitos limites complicados são facilmente calculados. Entretanto, é preciso ter sempre o cuidado de verificar se as hipóteses estão satisfeitas.
Muitas vezes, o limite a ser calculado aparece de maneira tal que aparentemente
não prevemos a utilização de uma das Regras de L'Hospital.
Esse é o caso do próximo exemplo.
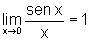 .
.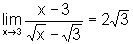 .
.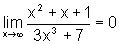 .
.
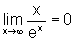 .
.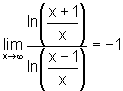 .
.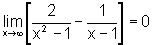 .
. .
.