![]() Um segmento
Um segmento 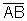 cujo comprimento é AB=a, está dividido em n partes iguais,
de modo que cada uma delas é a base de um triângulo isósceles
cujos ângulos da base medem 45o. Mostre que o limite
do comprimento da poligonal assim formada não é a,
apesar de, geometricamente, a poligonal tender ao segmento
cujo comprimento é AB=a, está dividido em n partes iguais,
de modo que cada uma delas é a base de um triângulo isósceles
cujos ângulos da base medem 45o. Mostre que o limite
do comprimento da poligonal assim formada não é a,
apesar de, geometricamente, a poligonal tender ao segmento 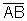 .
.
![]() Considere uma circunferência de raio R dado e o quadrado inscrito
nessa circunferência. Em seguida, considere a circunferência
inscrita nesse quadrado e o quadrado nela inscrito e assim sucessivamente.
Determine:
Considere uma circunferência de raio R dado e o quadrado inscrito
nessa circunferência. Em seguida, considere a circunferência
inscrita nesse quadrado e o quadrado nela inscrito e assim sucessivamente.
Determine:
a) a razão
entre a área de um dos círculos e a área do quadrado
nele inscrito;
b) a razão entre os comprimentos de duas circunferências
consecutivas;
c) o limite da soma das áreas de todos os círculos, quando
o número deles cresce infinitamente;
d) o limite da soma das áreas de todos os quadrados, quando o número
deles cresce infinitamente.
![]() Considere uma circunferência de raio r. Considere a seqüência
dos polígonos regulares de n lados que podem ser inscritos nessa
circunferência. Mostre que quando
Considere uma circunferência de raio r. Considere a seqüência
dos polígonos regulares de n lados que podem ser inscritos nessa
circunferência. Mostre que quando 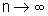 ,
o limite do perímetro do polígono de n lados é igual
ao comprimento da circunferência, isto é, 2pr.
,
o limite do perímetro do polígono de n lados é igual
ao comprimento da circunferência, isto é, 2pr.
![]() Considerando a mesma situação do problema anterior, mostre
que quando
Considerando a mesma situação do problema anterior, mostre
que quando 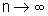 ,
o limite da área do polígono de n lados é igual à
área do círculo delimitado pela circunferência dada,
isto é, pr2.
,
o limite da área do polígono de n lados é igual à
área do círculo delimitado pela circunferência dada,
isto é, pr2.
