Vejamos então, se uma calculadora poderá, ou não, nos auxiliar.

- Observamos, neste caso, que podemos fazer x se aproximar de 0 pela esquerda ou pela direita, fazendo os cálculos uma única vez, pois na expressão de g, x aparece sempre ao quadrado.

x
±0,1	0,249843945
±0,01	0,2499984
±0,0001	0,25
±0,00001	0,25
±0,000001	0,2
±0,0000001	0
±0,00000001	0

Na calculadora observamos que, conforme x se aproxima de zero pela esquerda, ou pela direita, o correspondente valor de g(x) parece, inicialmente, se aproximar de 0,25, mas depois, pelo menos a partir de x=10^-6, algo está estranho... De fato, vemos que g(±0,000001) não é exatamente igual a zero, conforme a máquina forneceu. Isto nos leva a perceber que a ferramenta utilizada não tem precisão suficiente para resolver o nosso problema.

Talvez possamos encontrar uma outra máquina que tenha mais recursos, mas de toda forma, como também será limitada, em algum instante irá acontecer algo análogo e não nos ajudará a resolver o problema de descobrir para onde tende o valor de g(x) quando x se aproxima de zero, isto é qual é o valor de .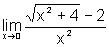

Esse exemplo é surpreendente, pois existe, muitas vezes, o costume de atribuir às máquinas - calculadoras ou computadores - um "poder" de cálculo muito superior ao nosso. Entretanto, esse tipo de dificuldade nos mostra como é importante não só conhecer, mas também compreender a Matemática, a fim de, inclusive, reconhecer as limitações de tais máquinas.