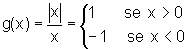Consideremos, por exemplo, .

Através da expressão 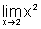, queremos, em primeiro lugar, dizer que 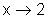, isto é x assume valores cada vez mais próximos de 2, mas não é 2. Em segundo lugar, para cada x, g(x), isto é, o correspondente valor de x², é um número que não é 4 - pois x não é 2 - e tende a algum valor que denominamos "limite de g(x) quando x tende a 2".

Consideremos

Novamente, a expressão nos diz que x não é zero, mas assume valores próximos de zero, tão próximos quanto quisermos e que, conforme x se aproxima de zero, 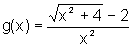, assume valores cujo limite, se é que existe algum, queremos encontrar.

Outro exemplo poderia ser .

Neste caso a expressão nos diz que x não é 3, mas se aproxima de 3 quanto quisermos. Também observamos que 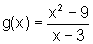não está definida em x=3. Entretanto, queremos saber para qual valor, se é que existe algum, para o qual a função tende, conforme x tende a 3.

Consideremos a função

Essa função não está definida em x=0, entretanto, podemos tentar calcular

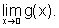
Conclusão: A notação 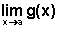significa que:

• a variável x se aproxima indefinidamente de a, por valores maiores ou menores do que a, mas não é igual a a;
  
  
• para cada valor de x, a variável dependente y=g(x) assume valores, que podem ou não se aproximar indefinidamente de um valor o qual, quando existe e é finito, é denominado .
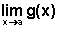
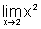
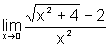
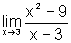