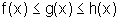Sejam f, g e h três funções tais que , para todo 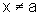. Se 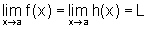, então existe 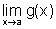e é também igual a L.

Antes de fazer a demonstração do Teorema, vamos visualizar aquilo que o teorema significa.

Na figura observamos que os gráficos - nas cores: verde e laranja - possuem um ponto em comum, que é a origem. A questão a ser analisada é a seguinte: se existir uma função que passe entre os gráficos das duas funções acima, qual seria o seu valor no ponto x=0?

É fácil perceber que essa nova função estará "espremida" entre as duas funções inicialmente dadas, em particular para x=0, devido à condição de seu gráfico estar entre os gráficos dados, resultando que o único valor possível para ela nesse ponto é y=0.

Assim, seu gráfico também passa pelo ponto (0,0).

Na figura temos o exemplo de duas funções, cujos gráficos estão em azul e rosa, que estão "espremidas" entre as duas funções inicialmente dadas, em particular no ponto x=0.

Vamos agora examinar uma situação semelhante, mas na qual as funções não estão definidas num certo ponto. Por exemplo, na figura abaixo:

Dadas as funções cujos gráficos estão em verde e laranja, observamos que ambas não estão definidas em x=1.

Agora, considerando uma outra função g, cujo gráfico esteja entre os dois gráficos dados e que também não esteja definida em x=1, a questão a ser colocada é a seguinte: qual é o valor de ?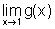

A resposta a essa pergunta é imediata usando o Teorema do Confronto: 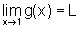, onde L é o limite para o qual tendem as duas funções dadas inicialmente.