a) a função
f + g tem limite em a e 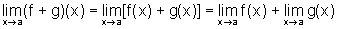 ;
;
b) a função
f . g tem limite em a e 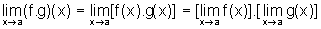 ;
;
c) se 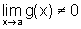 ,
então a função tem limite em a e
,
então a função tem limite em a e 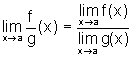 .
.
Demonstração:
- a) Sabendo que, por hipótese, f e g têm limite em um ponto a, isto é,
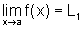 e
e 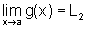 ,
,
queremos mostrar que
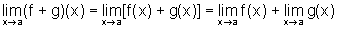 ,
,
ou seja:
para todo e >0, existe d >0 tal que
se 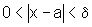 então
então 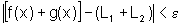
Observemos que, pela desigualdade triangular,
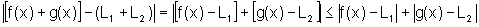
Como 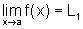 e
e 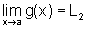 ,
,
os números
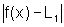 e
e 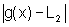 podem tornar-se arbitrariamente pequenos quando escolhemos x suficientemente
próximo de a. Em particular, eles podem tornar-se menores
do que
podem tornar-se arbitrariamente pequenos quando escolhemos x suficientemente
próximo de a. Em particular, eles podem tornar-se menores
do que 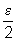 .
.
Assim, se 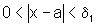 então
então 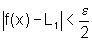 (1)
(1)
e se 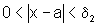 então
então
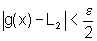 (2)
(2)
Tomando 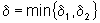 ,
ou seja, d é o menor dentre os valores
d1 e d2,
então sempre que
,
ou seja, d é o menor dentre os valores
d1 e d2,
então sempre que 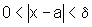 ,
valem (1) e (2).
,
valem (1) e (2).
Logo,
se 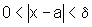 então
então 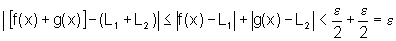
o que demonstra a parte a).
- b) Para demonstrar a propriedade relativa ao produto de funções, vamos primeiramente considerar um caso particular:
Se k é
uma função tal que 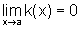 ,
enquanto que
,
enquanto que 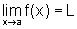 , então
, então
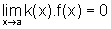 .
.
Como, por hipótese,
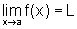 , segue que dado e
> 0, digamos e=1, existe d1>0
tal que
, segue que dado e
> 0, digamos e=1, existe d1>0
tal que
se 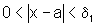 ,
então
,
então 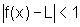
Mas então 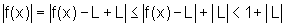
e, portanto,
se 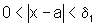 ,
então
,
então 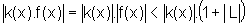 (3)
(3)
Assim, como 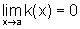 , dado
e >0 existe
d2 >0 tal que
, dado
e >0 existe
d2 >0 tal que
se 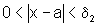 ,
então
,
então 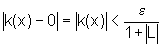 (4)
(4)
É preciso observar
que, como o erro permitido e > 0 é
qualquer, podemos tomar um erro menor 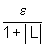 .
.
Agora, se 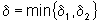 ,
então sempre que
,
então sempre que 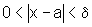 ,
valem (3) e (4), logo
,
valem (3) e (4), logo
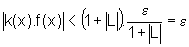 ,
,
ou seja,
se 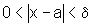 ,
temos
,
temos 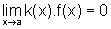
como queríamos mostrar.
Finalmente, para o produto de duas funções f . g,
sendo 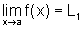 e
e 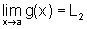 ,
,
observamos que:
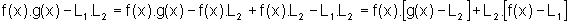
Como 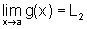 ,
segue que
,
segue que 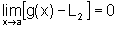 e, portanto,
pela demonstração do caso particular, temos que
e, portanto,
pela demonstração do caso particular, temos que 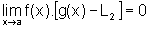 .
.
Da mesma forma, como
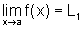 segue que
segue que 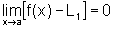 e, portanto, pela mesma razão temos
e, portanto, pela mesma razão temos 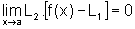 .
.
Logo, pela parte a),
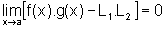 ou seja,
ou seja, 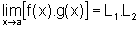
Como queríamos provar.
- c) Para demonstrar
a propriedade relativa ao quociente de funções, em primeiro
lugar, observamos que:
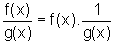 , isto é,
basta provar que, sendo
, isto é,
basta provar que, sendo 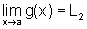 ,
então
,
então 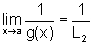 e depois utilizar o resultado obtido em b).
e depois utilizar o resultado obtido em b).
Para provar que 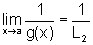 ,
consideremos o módulo seguinte:
,
consideremos o módulo seguinte:
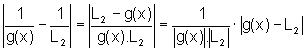 (5)
(5)
Como 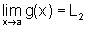 ,
,
dado 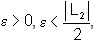 existe d1>0 tal que
existe d1>0 tal que
se 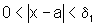 ,
então
,
então 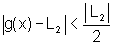
Assim para x
tal que 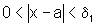 , temos
, temos
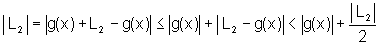
e daí:
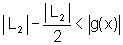
e, portanto, 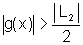 ou
seja,
ou
seja, 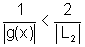
Dessa maneira, substituindo
na igualdade (5), para x tal que 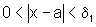 ,
temos que:
,
temos que:
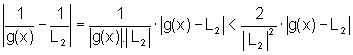 (6)
(6)
Novamente, como 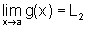 ,
dado
,
dado 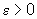 , existe
, existe 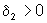 tal que
tal que
se 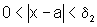 ,
então
,
então 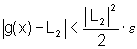 (7)
(7)
Tomando 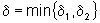 ,
ambas as desigualdades (6) e (7) são verdadeiras. Assim,
,
ambas as desigualdades (6) e (7) são verdadeiras. Assim,
se 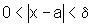 ,
então
,
então 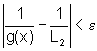 ,
o que significa que
,
o que significa que 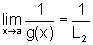 ,
como queríamos provar.
,
como queríamos provar.
 |
