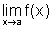, então existem
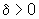e M >0 tais
que:
se 
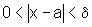então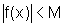 
.
Por hipótese,
temos que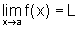 
.
Isso significa que:
dado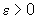 
, existe
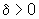tal que:
se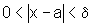 
então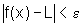 
A tese a ser
demonstrada é que existem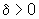
e M>0 tais que:
se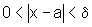 
então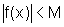 
.
Demonstração:
Se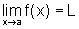 
,
então dado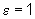 
,
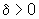existe tal que
se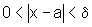
então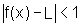 
ou seja, 
,
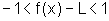ou ainda,
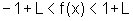
ou
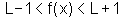
Dentre os números
(L-1) e (L+1) escolhemos o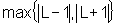 
.
Portanto, basta tomar
M = 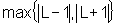, temos 
,
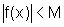sempre que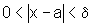 
.
 |
 |