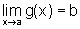Se f é uma função
contínua em x=b e 
,
então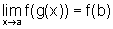 
.
Demonstração:
Dado e >0, queremos encontrar d >0, tal que,
se 
então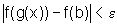 
.
Como por hipótese,
f é uma função contínua em b, temos que
f está definida em b e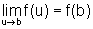 
,
ou seja, dado e >0, existe d1
>0 tal que
se 
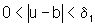então 
.
Como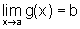 
,
existe d >0 tal que
se 
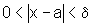então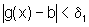 
.
Juntando os dois resultados, temos que:
se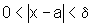 
então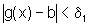 
e então 
,
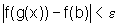ou seja,
,
como queríamos
demonstrar.
 |
 |