Conseqüência do Teorema do Confronto:
![]() Sejam f e g duas funções tais que
Sejam f e g duas funções tais que 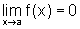 e g é
limitada.
e g é
limitada.
Então existe 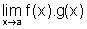 e
e  .
.
Demonstração:
Por hipótese,
g é limitada, ou seja, existe M real positivo, tal que 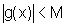 .
.
Também por
hipótese, 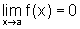 ,
ou seja, dado e >0, existe d
>0 tal que se:
,
ou seja, dado e >0, existe d
>0 tal que se:
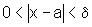 então
então 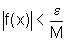 .
.
Logo, se 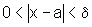 ,
temos:
,
temos:
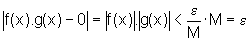
o que significa que
existe 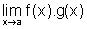 e
e
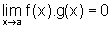 , o que conclui
a demonstração.
, o que conclui
a demonstração.
