Lema:
Se existe 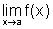 , então
existem
, então
existem 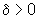 e M
> 0 tais que:
e M
> 0 tais que:
se 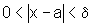 então
então 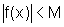 .
.
Isto significa que, se f tem limite no ponto a, então f é limitada numa vizinhança de a, ou seja, f é localmente limitada.
Teorema: Propriedades dos limites
Suponhamos que duas funções f e g tenham limites em um ponto a. Então temos:
a) a função
f+g tem limite em a e 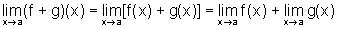 ;
;
b) a função
f.g tem limite em a e 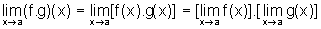 ;
;
c) se 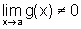 ,
então a função
,
então a função 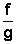 tem limite em a e
tem limite em a e 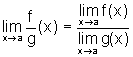 .
.
Teorema
do Confronto: Sejam f, g e h três funções tais
que 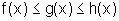 , para todo
, para todo
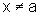 . Se
. Se 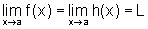 ,
então existe
,
então existe 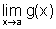 e é também igual a L.
e é também igual a L.
Conseqüência
do Teorema do Confronto: Sejam f e g duas funções
tais que 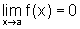 e g é
limitada.
Então existe
e g é
limitada.
Então existe 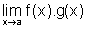 e
e 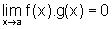 .
.
Teorema:
Se f é uma função
contínua em x=b e 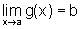 ,
então
,
então 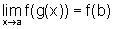 .
.

