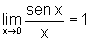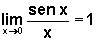
É preciso notar que o limite do numerador é 0, bem como o limite do denominador. Nesse caso o Teorema sobre as propriedades dos limites não pode ser aplicado.
Consideremos, inicialmente, que x se aproxima de 0 por valores maiores do que 0, isto é, x>0.
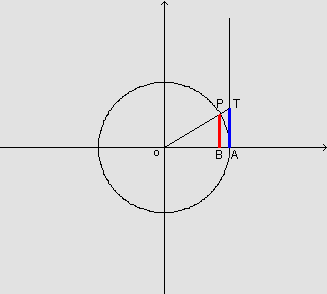
Temos então, a partir da figura:
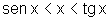
pois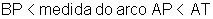 
,
uma vez que o número real x indica a medida do arco AP em
radianos.
Dividindo por sen x>0, pois x>0 e x "próximo" de 0, temos:
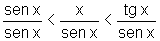
ou seja,
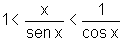
Tomando os inversos, as desigualdades mudam de sentido, ou seja,
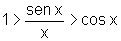
Quando x tende a 0 por valores maiores do que 0, isto é, x® 0+, pelo Teorema do Confronto, temos:
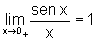
pois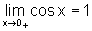 
e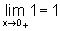 
Consideremos agora x se aproximando de 0 por valores menores
do que 0, isto é, x<0.
Temos então, a partir da figura:
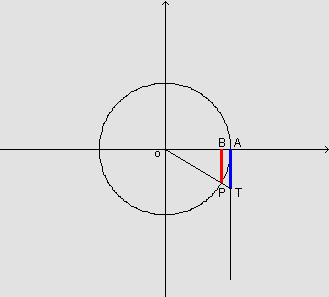
Como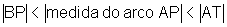 
, uma vez
que o número real x indica a medida do arco AP em radianos,
considerando as desigualdades sem módulos, temos:
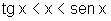
e dividindo por sen x<0, pois x<0 e x "próximo" de 0, temos:
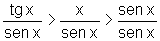
É conveniente observar que as desigualdades envolvem números que são positivos, pois cada termo é o quociente de dois negativos.
Temos então,
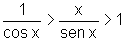
Tomando os inversos, as desigualdades mudam de sentido, ou seja,
Quando x tende a 0 por valores menores do que 0, isto é, x®0-, pelo Teorema do Confronto, temos:
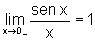
pois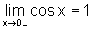 
e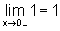 
.
Como os dois limites laterais tiveram como resultado o mesmo valor 1, temos, finalmente,
 |
 |