Exemplo 5 - Calculo Limites

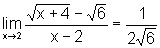
Para calcular este limite, observamos, em primeiro lugar que o Teorema sobre as propriedades dos limites não pode ser utilizado pois, embora o numerador e o denominador tenham limite, o limite do denominador é zero, contrariando uma das hipóteses do Teorema.

Entretanto, o numerador e o denominador tendem a zero e isso nos garante que 2 é raiz de ambos os termos da fração: (x-2) e 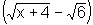. Esse fato nos indica o artifício a ser utilizado, pois, através dele obteremos o fator (x-2) em ambos os termos da fração.

Com efeito, multiplicando o numerador e o denominador pela expressão conjugada do numerador - que é onde temos uma diferença de radicais - nos livramos dessa diferença obtendo um fator que permite a simplificação da fração. Vejamos:

Dada a expressão a-b, a expressão conjugada é a+b e, reciprocamente, dada a+b, a conjugada é a-b.

Sempre é verdade que a²-b²=(a-b).(a+b)

É preciso notar que a simplificação por (x-2) foi possível, pois (x-2) não é igual a zero.

Com efeito, no cálculo de um limite, quando a variável x tende a 2, ela assume valores tão próximos de 2 quanto quisermos, mas nunca é exatamente 2.

Assim

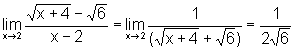
sendo que, na última igualdade utilizamos o Teorema sobre as propriedades dos limites, pois agora os limites de ambos os termos da fração existem e o do denominador não é zero.