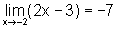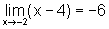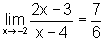
Observemos que a função cujo limite queremos calcular é o quociente entre dois termos. Onde cada um deles tem limite, ou seja:

Usando o Teorema sobre as propriedades dos limites, temos que, uma vez que existem os limites do numerador e do denominador, sendo o segundo diferente de zero, existe o limite do quociente, sendo este igual ao quociente dos limites. O que comprova o resultado acima.