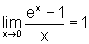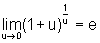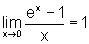
É preciso notar que o limite do numerador é 0, bem como o limite do denominador. Nesse caso o Teorema sobre as propriedades dos limites não pode ser aplicado.
A fim de calcular
esse limite, fazemos uma substituição de variável:
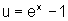 .
.
Daí, como ln é a função inversa da exponencial de base e,
x=ln(u+1)
e, quando x tende a 0, u tende a 0.
Substituindo, temos então:

Como ln é uma função contínua, para calcular o último limite usamos a propriedade sobre o limite de uma função contínua e obtemos:
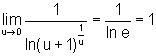
Logo,