![]()
Calcular limites desse tipo não gera problema algum, pois a função dada está definida no ponto para o qual a variável x está tendendo. Nesse caso, usamos o Teorema sobre as propriedades dos limites, que nos permite calcular o limite da soma, produto ou quociente de funções, desde que algumas hipóteses estejam satisfeitas.
![]()
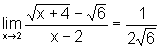
É preciso notar que o limite do numerador é 0, bem como
o limite do denominador. Nesse caso o Teorema sobre as propriedades dos
limites não pode ser aplicado.
![]()
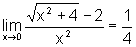
Novamente, não podemos aplicar o Teorema
sobre as propriedades dos limites.
![]() O limite fundamental
O limite fundamental 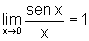
Não podemos esquecer que a variável x representa a medida
em radianos
de um arco. Para calcular esse limite precisamos do Teorema
do Confronto.
![]()

Esse limite necessita de um outro Teorema que é Conseqüência
do Teorema do Confronto.
![]()
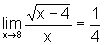
Como a função raiz quadrada é uma função
contínua em seu domínio e , então o numerador
tem
limite 2 e o denominador tende a 8, sendo, portanto, não nulo.
Podemos então aplicar o Teorema
sobre as propriedades dos limites para concluir o resultado.
![]()
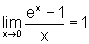
Já
sabemos que 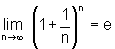 ,
onde n é um número natural que tende a infinito.
,
onde n é um número natural que tende a infinito.
A questão agora
é calcular um limite que também envolve o número
e, mas que tem a variável x percorrendo o conjunto
dos números reais. Para mostrar que 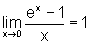 ,
mostramos
primeiro que
,
mostramos
primeiro que 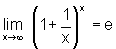 .
.
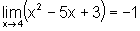
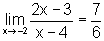
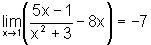
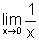 pois
pois 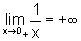 e
e 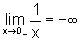 .
.