Para calcular a área do círculo procedemos da seguinte maneira:

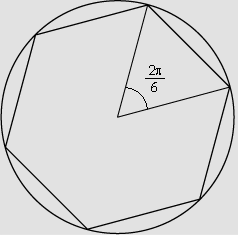
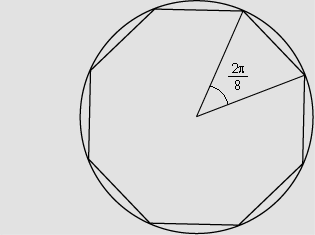
• Construímos um polígono regular de n lados, inscrito na circunferência.
• Dividimos o polígono em n triângulos isósceles, de modo que, em cada um deles, o ângulo oposto à base, que é um ângulo central, tem 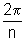radianos.

A área de cada um dos triângulos é

.

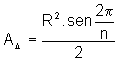E a soma das áreas de todos os triângulos é a área do polígono regular inscrito na circunferência, ou seja:

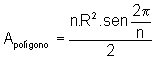
Fazendo o número de lados do polígono crescer infinitamente, vamos encontrar a área do círculo, ou seja:

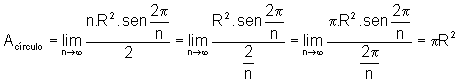
É preciso observar que 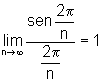pois é o limite fundamental, uma vez que quando , a fração 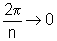.