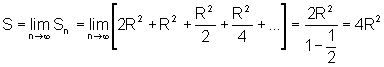A figura abaixo descreve a situação proposta:

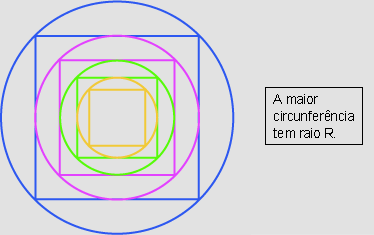
A partir da figura podemos construir duas tabelas: na primeira estão os dados relativos à seqüência de círculos e, na segunda tabela, aqueles relativos à seqüência de quadrados. A construção de tais tabelas é feita de maneira alternada, ou seja:

• conhecido o raio do círculo inicial, encontramos o lado do quadrado nele inscrito;
• a partir daí, conhecido o lado do quadrado, determinamos o raio do círculo inscrito nesse quadrado que é o segundo círculo;
• em seguida, determinamos o lado do quadrado inscrito no segundo círculo, que é o segundo quadrado;
• continuamos assim indefinidamente ...

	Raio	Perímetro	Área
1a circunferência	R1=R	2pR	pR2
2a circunferência	R2=	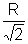2p
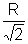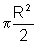3a circunferência	R3=	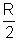pR
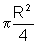4a circunferência	R4=

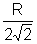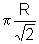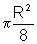	Lado	Perímetro	Área
1o quadrado	I1=R	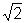4R	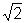2R2
2o quadrado	I2=R	4R	R2
3o quadrado	I3=
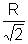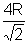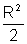4o quadrado	I4=	2R

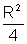a) a razão entre a área de um dos círculos e a área do quadrado nele inscrito:

Para cada círculo de raio r, o quadrado inscrito tem lado 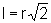. Assim sendo, o quociente das áreas entre esse círculo e esse quadrado é:

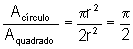
ou seja é um número que independe do tamanho do raio do círculo, ou do lado do quadrado nele inscrito.

b) a razão entre os comprimentos de duas circunferências consecutivas:

Dada uma circunferência de raio r, o quadrado nela inscrito tem lad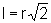o e a circunferência inscrita nesse quadrado tem raio .

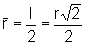Assim, a razão entre os comprimentos de duas circunferências consecutivas é dada por:

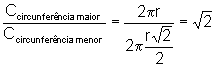
independentemente de quais duas circunferências da seqüência estejamos considerando, bastando apenas serem consecutivas.

c) o limite da soma das áreas de todos os círculos, quando o número deles cresce infinitamente:

Examinando a primeira tabela, observamos que as áreas dos círculos formam uma seqüência:

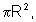
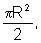
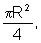
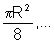
que é uma Progressão Geométrica de razão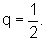

A soma dos infinitos termos dessa P.G. é dada por:

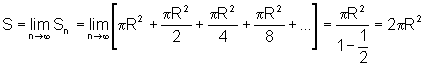
d) o limite da soma das áreas de todos os quadrados, quando o número deles cresce infinitamente:

Examinando a segunda tabela, observamos que as áreas dos quadrados formam uma seqüência:

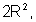
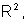
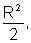
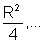
que é uma Progressão Geométrica de razão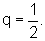

A soma dos infinitos termos dessa P.G. é dada por: